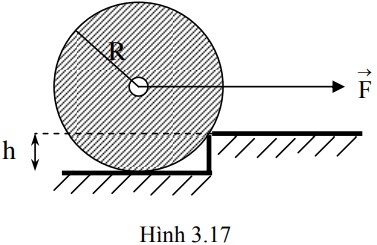
Bánh xe dạng đĩa tròn đồng nhất, bán kính R, khối lượng m đứng trước một bậc thềm có chiều cao h (hình 3.17). Phải đặt vào trục của bánh xe một lực F bằng bao nhiêu để nó có thể lên được thềm?

\(F \ge mg\frac{{\sqrt {h(2R - h)} }}{{R - h}}\)

\(F \ge mg\frac{{\sqrt {h(R - h)} }}{{R - h}}\)

\(F \ge mg\)

\(F \ge mg\sqrt {\frac{R}{{R - h}}}\)

Trả lời:

Đáp án đúng: A

Để bánh xe có thể lên được thềm, mômen của lực F quanh điểm tiếp xúc A giữa bánh xe và thềm phải lớn hơn hoặc bằng mômen của trọng lực mg quanh điểm A. Gọi O là tâm của bánh xe. Khoảng cách OA = R. Gọi B là hình chiếu của O lên mặt thềm. Khi đó OB = R - h. Mômen của trọng lực mg quanh A là: M_g = mg * AB, với AB = \(\sqrt{OA^2 - OB^2} = \sqrt{R^2 - (R-h)^2} = \sqrt{2Rh - h^2} = \sqrt{h(2R-h)}\) Mômen của lực F quanh A là: M_F = F * (R - h) Để bánh xe lên được thềm, ta có: M_F \(\ge\) M_g => F * (R - h) \(\ge\) mg * \(\sqrt{h(2R-h)}\) => F \(\ge\) mg * \(\frac{\sqrt{h(2R - h)}}{R - h}\) Vậy đáp án đúng là: \(F \ge mg\frac{{\sqrt {h(2R - h)} }}{{R - h}}\)

520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Phần 4

500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!

50 câu hỏi 60 phút

Bắt đầu thi

Câu hỏi liên quan

Câu 41:

Một khối trụ đặc đồng nhất, khối lượng m = 2 kg lăn không trượt trên mặt phẳng ngang dưới tác dụng của lực kéo F = 6N, đặt tại tâm khối trụ như hình 3.18. Bỏ qua ma sát cản lăn, gia tốc tịnh tiến của khối trụ là:

Lời giải:

Đáp án đúng: B

Áp dụng định luật II Newton cho chuyển động tịnh tiến của khối trụ: F = ma, từ đó suy ra a = F/m = 6N / 2kg = 3 m/s².

Câu 42:

Công thức nào sau đây tính chu kì dao động nhỏ của con lắc vật lý? (m: khối lượng của con lắc, d: khoảng cách từ khối tâm G đến trục quay, I: mômen quan tính của con lắc đối với trục quay, g là gia tốc trọng trường).

Lời giải:

Đáp án đúng: B

Công thức tính chu kì dao động nhỏ của con lắc vật lý là \(T = 2\pi \sqrt {\frac{I}{{mgd}}}\), trong đó:
- T là chu kì dao động.
- I là mômen quán tính của con lắc đối với trục quay.
- m là khối lượng của con lắc.
- g là gia tốc trọng trường.
- d là khoảng cách từ khối tâm G đến trục quay.

Do đó, đáp án đúng là phương án 2.

Câu 43:

Chọn phát biểu nào đúng dưới đây:

Lời giải:

Đáp án đúng: D

Phương trình chuyển động mô tả vị trí của vật theo thời gian, do đó cho phép xác định tính chất chuyển động (vị trí, vận tốc, gia tốc) tại một thời điểm bất kỳ. Phương trình quỹ đạo mô tả hình dạng đường đi của vật. Nếu biết phương trình chuyển động, ta có thể khử thời gian để tìm ra phương trình quỹ đạo. Tuy nhiên, việc tìm phương trình chuyển động từ phương trình quỹ đạo thường khó khăn hơn và không phải lúc nào cũng thực hiện được. Vì vậy, A, B, và C đều đúng.

Câu 44:

Chất điểm chuyển động có đồ thị như hình 1.2. Tại thời điểm t = 2s, chất điểm đang:

Lời giải:

Đáp án đúng: D

Đồ thị hình 1.2 biểu diễn sự phụ thuộc của vận tốc vào thời gian (v(t)). Tại thời điểm t = 2s, đường thẳng trên đồ thị nằm ngang, điều này cho thấy vận tốc của chất điểm không thay đổi theo thời gian. Do đó, chất điểm đang chuyển động đều.

Câu 45:

Chất điểm chuyển động trong mặt phẳng Oxy với phương trình: \(\left\{ \begin{array}{l} x = 3{t^2} - \frac{4}{2}{t^3}\\ y = 8t \end{array} \right.\)(SI). Tính độ lớn của gia tốc lúc t = 1s.

Lời giải:

Đáp án đúng: A

Để tìm gia tốc, ta cần tính đạo hàm cấp hai của x và y theo thời gian t.

Phương trình chuyển động:
x = 3t² - (4/2)t³ = 3t² - 2t³
y = 8t

Tính vận tốc theo x và y:
vx = dx/dt = 6t - 6t²
vy = dy/dt = 8

Tính gia tốc theo x và y:
ax = dvx/dt = 6 - 12t
ay = dvy/dt = 0

Tại t = 1s:
ax = 6 - 12(1) = -6 m/s²
ay = 0 m/s²

Độ lớn của gia tốc là:
a = √(ax² + ay²) = √((-6)² + 0²) = √36 = 6 m/s²

Tuy nhiên, không có đáp án nào trùng với kết quả tính toán. Xem xét lại đề bài và các phương án, có thể có sai sót trong đề bài hoặc các phương án trả lời. Hoặc có thể có một cách hiểu khác về đề bài mà dẫn đến một trong các đáp án đã cho.

Nếu ta giả sử có một sự nhầm lẫn nhỏ và đáp án gần đúng nhất, ta sẽ chọn đáp án gần với kết quả 6 m/s² nhất. Trong các đáp án đã cho, không có đáp án nào gần đúng với 6 m/s². Vì vậy, ta cần xem xét lại cách giải hoặc đề bài.

Tuy nhiên, nếu chúng ta tính toán lại một cách cẩn thận và giả sử không có sai sót trong đề bài, chúng ta vẫn thu được kết quả là 6 m/s². Vì không có đáp án nào đúng, nên ta sẽ đánh dấu đây là một câu hỏi có vấn đề.

Câu 46:

Chất điểm chuyển động trong mặt phẳng Oxy với phương trình: \(\left\{ \begin{array}{l} x = 3{t^2} - \frac{4}{2}{t^3}\\ y = 8t \end{array} \right.\) (SI). Gia tốc của chất điểm triệt tiêu vào thời điểm nào?

Lời giải: