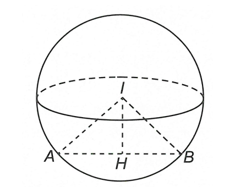
Trong không gian Oxyz, cho điểm \(I\left( 1;-2;3 \right).\) Viết phương trình mặt cầu tâm I, cắt trục Ox tại hai điểm A và B sao cho \(AB=2\sqrt{3}.\)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn A
Gọi H là trung điểm \(AB\Rightarrow IH\bot AB\) tại \(H\Rightarrow IH={{d}_{\left( I;\left( AB \right) \right)}}={{d}_{\left( I;Ox \right)}}\)
Lấy \(M\left( 2;0;0 \right)\in Ox\Rightarrow IH={{d}_{\left( I,Ox \right)}}\)\( =\frac{\left| \left[ \overrightarrow{IM},\overrightarrow{i} \right] \right|}{\overrightarrow{i}}=\sqrt{3}.\)
Bán kính mặt cầu cần tìm là \(R=IA=\sqrt{I{{H}^{2}}+H{{A}^{2}}}=4.\)
Vậy phương trình mặt cầu cần tìm là \(~{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=16.\)
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Phú Lâm