Có bao nhiêu số nguyên dương \(y\) nhỏ hơn \(500\) sao cho ứng với mỗi \(y\) tồn tại ít nhất 9 số nguyên \(x\) thỏa mãn bất phương trình sau \({{x}^{4}}+2{{x}^{2}}-y+1\le {{\log }_{2}}\frac{\sqrt{2y+1}}{{{x}^{2}}+1}\)?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có bất phương trình \(\Leftrightarrow {{\left( {{x}^{2}}+1 \right)}^{2}}-y\le {{\log }_{2}}{{\left( 2y+1 \right)}^{\frac{1}{2}}}-{{\log }_{2}}\left( {{x}^{2}}+1 \right)\)
\(\Leftrightarrow 2{{\left( {{x}^{2}}+1 \right)}^{2}}-2y\le {{\log }_{2}}\left( 2y+1 \right)-{{\log }_{2}}{{\left( {{x}^{2}}+1 \right)}^{2}}\).
\(\Leftrightarrow 2{{\left( {{x}^{2}}+1 \right)}^{2}}+{{\log }_{2}}{{\left( {{x}^{2}}+1 \right)}^{2}}\le {{\log }_{2}}\left( 2y+1 \right)+2y+1-1\)
\(\Leftrightarrow 2{{\left( {{x}^{2}}+1 \right)}^{2}}+{{\log }_{2}}\left[ 2{{\left( {{x}^{2}}+1 \right)}^{2}} \right]\le {{\log }_{2}}\left( 2y+1 \right)+\left( 2y+1 \right)\)
Xét hàm đặc trưng \(f\left( t \right)=t+{{\log }_{2}}t\) với \(t\in \left( 0;+\infty \right)\).
Ta có: \(f'\left( t \right)=1+\frac{1}{t\ln 2}>0\)\(\forall t>0\Rightarrow f\left( t \right)\) đồng biến trên \(\left( 0;+\infty \right)\).
Do đó \(\left( * \right)\Leftrightarrow 2{{\left( {{x}^{2}}+1 \right)}^{2}}\le 2y+1\) \(\Leftrightarrow 2{{x}^{4}}+4{{x}^{2}}+1\le 2y\).
Đặt \(g\left( x \right)=2{{x}^{4}}+4{{x}^{2}}+1\) với \(x\in \mathbb{R}\).
Ta có: \(g'\left( x \right)=8{{x}^{3}}+8x\). Cho \(g'\left( x \right)=0\Leftrightarrow x=0\).
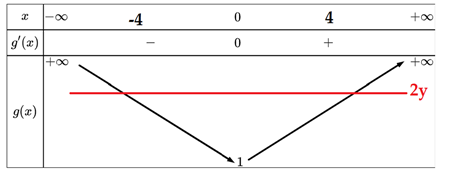
Lập bảng biến thiên ta có:
Dựa vào bảng biến thiên ta thấy \(2y\ge g(4)={{2.4}^{4}}+{{4.4}^{2}}+1=577\)\(\Rightarrow y\ge \frac{577}{2}=288,5\).
Do
\(\left\{ \begin{align} & y\in {{\mathbb{Z}}^{+}} \\ & y<500 \\ \end{align} \right.\)
\(\Rightarrow y\in \left\{ 289;290;...;499 \right\}\) \(\Rightarrow \) Có tất cả \(211\) giá trị nguyên thỏa mãn.
Chọn B
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Trần Cao Vân
Câu hỏi liên quan
-
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Góc giữa 2 đường thẳng \(B{A}'\) và \({B}'{D}'\) bằng?
-
Cho \(a,b,c\) là các số dương khác \(1\) thoả mãn \({{\log }_{a}}b=2,\,{{\log }_{b}}c=3\). Tính giá trị của \({{\log }_{c}}a\)?
-
Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các đường thẳng \(y={{x}^{3}}\) & \(y=2{{x}^{2}}\) là?
-
Trong không gian \(Oxyz\), cho 2 đường thẳng \({{d}_{1}}:\frac{x-1}{2}=\frac{y}{1}=\frac{z+2}{-1}\) và \({{d}_{2}}:\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-2}{-2}\). Gọi \(\Delta \) là đường thẳng song song với mặt phẳng \(\left( P \right):x+y+z-7=0\) và cắt \({{d}_{1}},\,{{d}_{2}}\) lần lượt tại hai điểm \(A,\,B\) sao cho \(AB\) ngắn nhất. phương trình của đường thẳng \(\Delta \) là?
-
Tìm mặt phẳng chứa \(\left( \Delta \right)\) và song song với \(AB\) có phương trình là?
-
Trong không gian \(Oxyz\), mp \(\left( Oxz \right)\) có phương trình là?
-
Xét tích phân sau đây \(I=\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+\cos x}dx}\). Nếu đặt \(t=\cos x\) thì tích phân \(I\) trở thành?
-
Tính đạo hàm của hàm số sau đây \(y={{3}^{2x+1}}\)?
-
Có tất cả bao nhiêu cặp số nguyên dương \(\left( x;y \right)\) thỏa mãn điều kiện \(x\le 2022\) và \(3\left( {{9}^{y}}+2y \right)+2\le x+{{\log }_{3}}{{\left( x+1 \right)}^{3}}\)?
-
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có BBT như sau:
Số nghiệm thuộc khoảng \(\left( -\infty ;\ln 2 \right)\) của phương trình \(2020f\left( 1-{{e}^{x}} \right)-2021=0\) là?
-
Số giá trị nguyên nhỏ hơn \(2020\) của tham số \(m\) để phương trình sau \({{{\log }_{6}}\left( 2020x+m \right)={{\log }_{4}}\left( 1010x \right)}\) có nghiệm là?
-
Trong không gian với hệ toạ độ \(Oxyz\), cho điểm \(M\left( 2;-3;1 \right)\) và mp \(\left( \alpha \right):x+3y-z+2=0\). Đường thẳng \(d\) đi qua điểm \(M\) và vuông góc với mặt phẳng \(\left( \alpha \right)\) có phương trình là?
-
Với \(a\) là số thực dương tuỳ ý, giá trị của \(\log \left( \frac{10}{{{a}^{2}}} \right)\) bằng?
-
Cho số phức \(z=\frac{5}{2}-\frac{1}{2}i\). Tìm tọa độ điểm \(M\) biểu diễn số phức \(z\) là?
-
Cho hình nón đỉnh \(S\) có bán kính đáy bằng \(5a\). Gọi \(A\) và \(B\) là 2 điểm thuộc đường tròn đáy sao cho \(AB=8a\). Biết mặt phẳng \(\left( SAB \right)\) tạo với đáy một góc \({{60}^{0}}\), diện tích xung quanh \(S\) của hình nón đã cho bằng?
-
Cho hàm số \(f\left( x \right)=\,{{x}^{4}}+2{{x}^{2}}+1\). Có bao nhiêu giá trị nguyên của tham số \(m\in \left[ 0\,;\,10 \right]\) để hàm số \(g\left( x \right)=f\left( 3\left| x-m \right|+{{m}^{2}} \right)\) nghịch biến trên khoảng \(\left( -\infty \,;\,1 \right)\)?
-
Nguyên hàm của hàm số sau đây \(f(x)={{3}^{x}}-x\) là?
-
Cho hàm số \(f\left( x \right)\) có đạo hàm và đồng biến trên \(\left[ 1;4 \right],\) thoả mãn \(x+2xf\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}\) với mọi \(x\in \left[ 1;4 \right].\) Biết rằng \(f\left( 1 \right)=\frac{3}{2},\) tính tích phân của \(I=\int\limits_{1}^{4}{f\left( x \right)}dx\)?
-
Họ nguyên hàm của hàm số sau đây \(f\left( x \right)=3{{x}^{2}}-\frac{1}{x}+\frac{2}{{{x}^{2}}}\) là?
-
Cho tập hợp \(A\) có \(7\) phần tử. Cho biết số tập con có \(3\) phần tử của tập \(A\) là?
