Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( x-1 \right).\log \left( {{e}^{-x}}+m+2023 \right)=x-2\) có hai nghiệm thực phân biệt?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐiều kiện: \({{e}^{-x}}+m+2023>0\) (*).
Vì \(x=1\) không là nghiệm nên phương trình nên:
Với \(x\ne 1\), \(\log ({{e}^{-x}}+m+2023)=\frac{x-2}{x-1}\Leftrightarrow {{e}^{-x}}+m+2023={{10}^{\frac{x-2}{x-1}}}>0\)( thỏa mãn (*)) \(\Leftrightarrow m+2023={{10}^{\frac{x-2}{x-1}}}-{{e}^{-x}}\).
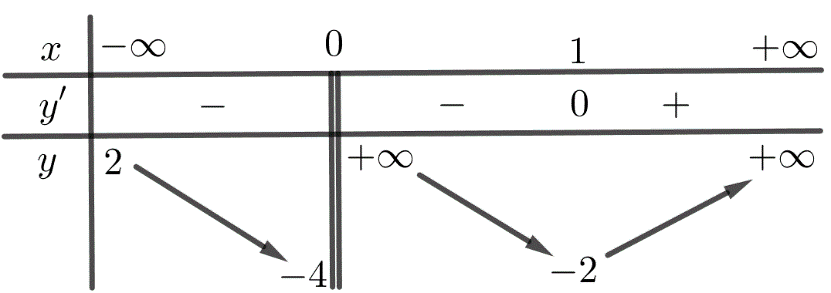
Đặt \(y=g(x)={{10}^{\frac{x-2}{x-1}}}-{{e}^{-x}}\)
Ta có: \({y}'=\frac{1}{{{(x-1)}^{2}}}{{10}^{\frac{x-2}{x-1}}}\ln 10+{{e}^{-x}}>0,\forall x\ne 1\)
Bảng biến thiên:
Vậy phương trình có 2 nghiệm thực phân biệt khi \(-\frac{1}{e}<m+2023<10\). Chọn D.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Vụ Bản



.PNG)

.PNG)
.PNG)
.PNG)