Cho một tấm nhôm hình vuông cạnh \(1\left( m \right)\) như hình vẽ bên.
.PNG)
Người ta cắt phần tô đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng \(x\,\left( m \right)\) sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Giá trị của \(x\) để khối chóp nhận được có thể tích lớn nhất là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.PNG)
Từ hình vuông ban đầu ta tính được \(OM=\frac{x}{2},\,{{S}_{1}}M={{S}_{1}}O-OM=\frac{\sqrt{2}-x}{2}\). (\)0<x<\sqrt{2}\))
Khi gấp thành hình chóp \(S.ABCD\) thì \({{S}_{1}}\equiv S\) nên ta có \(SM={{S}_{1}}M\).
Từ đó \(SO=\sqrt{S{{M}^{2}}-O{{M}^{2}}}=\frac{\sqrt{2-2\sqrt{2}x}}{2}\). (Điều kiện \(0<x<\frac{\sqrt{2}}{2}\) )
Thể tích khối chóp \(S.ABCD\): \({{V}_{S.ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SO=\frac{1}{6}{{x}^{2}}\sqrt{2-2\sqrt{2}x}=\frac{1}{6}\sqrt{2{{x}^{4}}-2\sqrt{2}{{x}^{5}}}\).
Ta thấy \({{V}_{SABCD}}\) lớn nhất khi \(f\left( x \right)=2{{x}^{4}}-2\sqrt{2}{{x}^{5}},\)\)0<x<\frac{\sqrt{2}}{2}\) đạt giá trị lớn nhất
Ta có \({f}'\left( x \right)=8{{x}^{3}}-10\sqrt{2}{{x}^{4}}=2{{x}^{3}}\left( 4-5\sqrt{2}x \right)\)
\({f}'\left( x \right)=0\)
\(\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\frac{2\sqrt{2}}{5} \\ \end{align} \right.\)
Bảng biến thiên
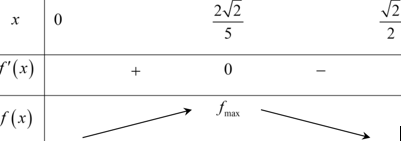
Vậy: \({{V}_{S.ABCD}}\) lớn nhất khi và chỉ khi \(x=\frac{2\sqrt{2}}{5}\).
Chọn D
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Vụ Bản
Câu hỏi liên quan
-
Cho hàm số bậc bốn \(f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e\ \left( a,b,c,d,e\in \mathbb{R} \right)\) và hàm số bậc ba \(g\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+px+q\ \left( m,n,p,q\in \mathbb{R} \right)\) có đồ thị \(y=f'\left( x \right)\) và \(y=g'\left( x \right)\) như hình vẽ bên dưới.
.PNG)
Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y=f\left( x \right)\) và \(y=g\left( x \right)\) bằng 96 và \(f\left( 2 \right)=g\left( 2 \right)\). Diện tích hình phẳng giới hạn bởi các đường \(y=f\left( x \right),y=g\left( x \right)\) và \(x=0,\ x=2\) bằng
-
Đường cong trong hình vẽ bên là đồ thị hàm số nào trong bốn hàm số dưới đây?
-
Cho hàm số bậc bốn \(y=f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e\) thỏa mãn \(f\left( 0 \right)=3f\left( 2 \right)=-3\) và có đồ thị hàm số \(y={f}'\left( x \right)\) như hình bên dưới.
.PNG)
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( -20;20 \right)\) để hàm số \(g\left( x \right)=f\left[ 4f\left( x \right)-f''\left( x \right)+m \right]\) đồng biến trên khoảng \(\left( 0;1 \right)?\)
-
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( -10;6;-2 \right),B\left( -5;10;-9 \right)\) và mặt phẳng \(\left( \alpha \right):2x-2y-z+12=0\). Điểm \(M\left( a;b;c \right)\) thuộc \(\left( \alpha \right)\) sao cho \(MA,MB\) tạo với \(\left( \alpha \right)\) các góc bằng nhau và biểu thức \(T=2M{{A}^{2}}-M{{B}^{2}}\) đạt giá trị nhỏ nhất. Tổng \(a+b+c\) bằng
-
Hàm số nào dưới đây có bảng biến thiên như hình sau
-
Cho khối lăng trụ tam giác có chiều cao \(h=3\) và đáy là tam giác đều cạnh \(a=2.\) Thể tích khối lăng trụ đã cho bằng
-
Cho số thực \(a\) thỏa mãn \({{a}^{3}}>{{a}^{\pi }}\). Mệnh đề nào sau đây đúng?
-
Số nghiệm của phương trình \({{\log }_{3}}\left( {{x}^{2}}+4x \right)\)\( +{{\log }_{\frac{1}{3}}}\left( 3x+6 \right)=0\) là
-
Năm \(2023\) một hãng xe niêm yết giá bán loại xe X là \(750.000.000\) đồng và dự định trong \(10\) năm tiếp theo, mỗi năm giảm \(2%\) giá bán so với giá bán của năm liền trước. Theo dự định đó, năm \(2030\) hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu? (kết quả làm tròn đến hàng nghìn)
-
Cho hàm số \(y=f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ bên. Số giá trị nguyên dương của tham số \(m\) để phương trình \(f\left( x \right)=m\) có hai nghiệm phân biệt là
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
Trong không gian \(Oxyz,\) cho \(\vec{a}=\left( 1;-2;3 \right)\) và \(\vec{b}=\left( -1;3;0 \right)\). Vectơ \(\vec{a}-\vec{b}\) có tọa độ là
-
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 1;8 \right]\) và thỏa mãn
\(\int\limits_{1}^{2}{{{\left[ f\left( {{x}^{3}} \right) \right]}^{2}}}dx+2\int\limits_{1}^{2}{f\left( {{x}^{3}} \right)}dx-\frac{4}{3}\int\limits_{1}^{8}{f\left( x \right)}dx=-\frac{247}{15}\).
Giả sử \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ 1;8 \right].\)Tích phân \(\int\limits_{1}^{8}{xF'\left( x \right)}dx\) bằng
-
Cho hình hộp chữ nhật \(ABCD.{A}'{B}'{C}'{D}'\) có \(A{A}'=AD=a\), \(AB=a\sqrt{2}\) (tham khảo hình vẽ). Góc giữa đường thẳng \({A}'C\) và mặt phẳng \(\left( ABB'A' \right)\) bằng
.PNG)
-
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị là đường cong như hình vẽ bên. Điểm cực đại của đồ thị hàm số đã cho là
.PNG)
-
Cho khối chóp có thể tích \(4{{a}^{3}}\) và diện tích đáy \(4{{a}^{2}}.\) Chiều cao của khối chóp đã cho bằng
-
Trong không gian \(Oxyz,\) vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng \(\left( Oxy \right)?\)
-
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({{x}^{2}}f\left( {{x}^{5}} \right)+xf\left( 1-{{x}^{4}} \right)=-3{{x}^{4}}+x+3,\,\forall x\in \mathbb{R}\). Khi đó \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x}\) bằng
-
Trong các khẳng định sau, khẳng định nào sai?
-
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-6z-5=0.\) Tâm của mặt cầu \(\left( S \right)\) có tọa độ là
