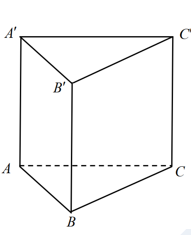
Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh đều bằng \(2\) (tham khảo hình bên dưới)
Khoảng cách từ \(B\) đến mặt phẳng \(\left( AC{C}'{A}' \right)\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai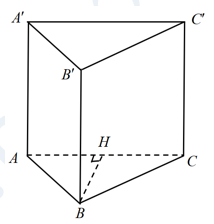
Trong mặt phẳng \(\left( ABC \right)\) kẻ \(BH\bot AC\).
Vì \(ABC.{A}'{B}'{C}'\) là hình lăng trụ tam giác đều \({A}'A\bot \left( ABC \right)\,\,\Rightarrow \,\,{A}'A\bot BH\).
Vậy
\(\left\{ \begin{align} & BH\bot AC\,,\,\,BH\bot {A}'A\, \\ & AC\,,\,{A}'A\,\subset \,\left( AC{C}'{A}' \right) \\ & AC\,\cap \,{A}'A=A\, \\ \end{align} \right.\)
\(\,\Rightarrow \,BH\bot \,\left( AC{C}'{A}' \right)\,\,\Rightarrow \,\,d\left( B,\left( AC{C}'{A}' \right) \right)=BH\).
\(\Delta \,ABC\) đều cạnh bằng \(2\) nên \(BH=\frac{2\sqrt{3}}{2}=\sqrt{3}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Herman-Gmeiner
















