Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB=1,AD=AA'=\sqrt{3}\). Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và \(BC\). Góc giữa hai đường thẳng \(MN\) và \(AC\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai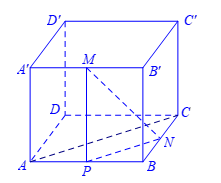
Xét tam giác \(ABC\) vuông tại \(B\Rightarrow AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2\).
Gọi \(P\) là trung điểm của \(AB\).
Khi đó \(NP\) là đường trung bình của tam giác \(ABC\).
\(\Rightarrow \left\{ \begin{align} & NP\text{//}AC \\ & NP=\frac{1}{2}AC=1 \\ \end{align} \right.\)
Do \(NP\text{//}AC\) nên \(\widehat{(MN,AC)}=\widehat{(MN,NP)}=\widehat{MNP}\).
Do \(M,P\) lần lượt là trung điểm của \({A}'{B}'\) và \(AB\Rightarrow MP=A{A}'=\sqrt{3}\).
Xét tam giác \(MNP\) vuông tại \(P\) có \(\tan \widehat{MNP}=\frac{MP}{NP}=\sqrt{3}\Rightarrow \widehat{MNP}={{60}^{0}}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Herman-Gmeiner