Trong không gian \(Oxyz\), cho mặt cầu \((S):{{(x+1)}^{2}}+{{(y-1)}^{2}}+{{z}^{2}}=4\) và hai điểm \(A(1\,;\,2\,;\,4)\), \(B(0\,;\,0\,;\,1)\). Mặt phẳng \((P):ax+by+cz+3=0\) \((a,b,c\in \mathbb{R})\) đi qua \(A,B\) và cắt \((S)\) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Giá trị của \(a+b+c\) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai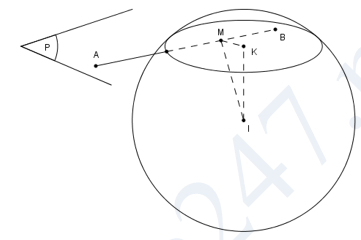
Mặt cầu \((S)\) có tâm \(I(-1\,;\,1\,;\,0)\) và bán kính \(R=2\).
Ta có \(IA=\sqrt{21}\), \(IB=\sqrt{3}\) nên \(A\) nằm ngoài \((S)\), \(B\) nằm trong \((S)\). Do đó mặt phẳng \((P)\) luôn cắt \((S)\) theo một đường tròn \((C)\) tâm \(K\) bán kính \(r\).
Gọi \(M\) là hình chiếu vuông góc của \(I\) trên đường thẳng \(AB\).
Ta có \(IK=\text{d}(I,(P))\) và \({{r}^{2}}={{R}^{2}}-I{{K}^{2}}\).
Ta có \(IK\bot (P)\) \(\Rightarrow IK\le IM\) \(\Rightarrow {{r}^{2}}\ge {{R}^{2}}-I{{M}^{2}}\).
Đẳng thức xảy ra khi \(IM\bot (P)\). Khi đó
\({{\vec{n}}_{(P)}}=(\overrightarrow{AB}\wedge \overrightarrow{IA})\wedge \overrightarrow{AB}=(12;-18;8).\)
Vì \(R;IM\) không đổi nên \(r\) có giá trị nhỏ nhất bằng \(\sqrt{{{R}^{2}}-I{{M}^{2}}}\).
Khi đó phương trình mặt phẳng \((P)\) là
\(\begin{align} & \text{ }12(x-0)-18(y-0)+8(z-1)=0 \\ & \Leftrightarrow ~\text{ }12x-18y+8z-8=0 \\ & \Leftrightarrow ~\text{ }-\frac{9}{2}x+\frac{27}{4}y-3z+3=0. \\ \end{align}\)
Vậy \(a+b+c=-\frac{9}{2}+\frac{27}{4}-3=-\frac{3}{4}\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Herman-Gmeiner