Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và SO = a. Khoảng cách giữa SC và AB bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai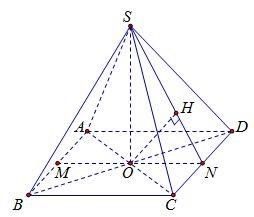
Gọi M,N lần lượt là trung điểm của các cạnh AB; CDCD; H là hình chiếu vuông góc của O trên SN
Vì AB// CD nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizamaabm % aabaGaamyqaiaadkeacaGGSaGaai4uaiaacoeaaiaawIcacaGLPaaa % cqGH9aqpcaWGKbWaaeWaaeaacaWGbbGaamOqaiaacYcacaGGOaGaam % 4uaiaadoeacaWGebGaaiykaaGaayjkaiaawMcaaiabg2da9iaadsga % daqadaqaaiaad2eacaGGSaGaaiikaiaadofacaWGdbGaamiraiaacM % caaiaawIcacaGLPaaacqGH9aqpcaaIYaGaamizamaabmaabaGaam4t % aiaacYcacaGGOaGaam4uaiaadoeacaWGebGaaiykaaGaayjkaiaawM % caaaaa!57EE! d\left( {AB,SC} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\)
Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadoeacaWGebGaeyyPI4Laam4uaiaad+eaaeaacaWGdbGaamir % aiabgwQiEjaad+eacaWGobaaaiaawUhaaiabgkDiElaadoeacaWGeb % GaeyyPI4LaaiikaiaadofacaWGpbGaamOtaiaacMcacqGHshI3caWG % dbGaamiraiabgwQiEjaad+eacaWGibaaaa!51A2! \left\{ \begin{array}{l} CD \bot SO\\ CD \bot ON \end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH\)
Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadoeacaWGebGaeyyPI4Laam4taiaadIeaaeaacaWGpbGaamis % aiabgwQiEjaadofacaWGobaaaiaawUhaaiabgkDiElaad+eacaWGib % GaeyyPI4LaaiikaiaadofacaWGdbGaamiraiaacMcacqGHshI3caWG % KbWaaeWaaeaacaWGpbGaai4oaiaacIcacaWGtbGaam4qaiaadseaca % GGPaaacaGLOaGaayzkaaGaeyypa0Jaam4taiaadIeacaGGUaaaaa!57E2! \left\{ \begin{array}{l} CD \bot OH\\ OH \bot SN \end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.\)
Tam giác SON vuông tại O nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaam4taiaadIeadaahaaWcbeqaaiaaikdaaaaaaOGaeyyp % a0ZaaSaaaeaacaaIXaaabaGaam4taiaad6eadaahaaWcbeqaaiaaik % daaaaaaOGaey4kaSYaaSaaaeaacaaIXaaabaGaam4taiaadofadaah % aaWcbeqaaiaaikdaaaaaaOGaeyypa0ZaaSaaaeaacaaIXaaabaWaaS % aaaeaacaWGHbWaaWbaaSqabeaacaaIYaaaaaGcbaGaaGinaaaaaaGa % ey4kaSYaaSaaaeaacaaIXaaabaGaamyyamaaCaaaleqabaGaaGOmaa % aaaaGccqGH9aqpdaWcaaqaaiaaiwdaaeaacaWGHbWaaWbaaSqabeaa % caaIYaaaaaaakiabgkDiElaad+eacaWGibGaeyypa0ZaaSaaaeaaca % WGHbaabaWaaOaaaeaacaaI1aaaleqaaaaaaaa!5489! \frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{\frac{{{a^2}}}{4}}} + \frac{1}{{{a^2}}} = \frac{5}{{{a^2}}} \Rightarrow OH = \frac{a}{{\sqrt 5 }}\)
Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizamaabm % aabaGaamyqaiaadkeacaGGSaGaai4uaiaacoeaaiaawIcacaGLPaaa % cqGH9aqpcaaIYaGaam4taiaadIeacqGH9aqpdaWcaaqaaiaaikdaca % WGHbWaaOaaaeaacaaI1aaaleqaaaGcbaGaaGynaaaaaaa!43FF! d\left( {AB,SC} \right) = 2OH = \frac{{2a\sqrt 5 }}{5}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Tuyển chọn số 3
Câu hỏi liên quan
-
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
.png)
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadggacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaamOy % aiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGJbGaamiEai % abgUcaRiaaigdaaaa!42EC! y = a{x^3} + b{x^2} + cx + 1\) có bảng biến thiên như sau:
.png)
Mệnh đề nào dưới đây đúng?
-
Tính tích phân \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaada % qadaqaaiaaikdacaWGHbGaamiEaiabgUcaRiaadkgaaiaawIcacaGL % PaaacaqGKbGaamiEaaWcbaGaaGymaaqaaiaaikdaa0Gaey4kIipaaa % a!41A8! \int\limits_1^2 {\left( {2ax + b} \right){\rm{d}}x} \)
-
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ
.png)
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadAgadaqadaqaaiaadIhadaahaaWcbeqaaiaaikdaaaaakiaa % wIcacaGLPaaaaaa!3C5C! y = f\left( {{x^2}} \right)\) có bao nhiêu khoảng nghịch biến.
-
Cho hàm số y = f(x). Khẳng định nào sau đây là đúng?
-
Lớp 11A có 40 học sinh trong đó có 12 học sinh đạt điểm tổng kết môn Hóa học loại giỏi và 13 học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là 0,5. Số học sinh đạt điểm tổng kết giỏi cả hai môn Hóa học và Vật lí là
-
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaSaaaeaacaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaaGOnaiaadIhacqGHRaWkcaaI4a % aabaGaaGinaiaadIhacqGHsislcaaIXaaaaiabgwMiZkaaicdaaaa!45E6! {\log _2}\frac{{{x^2} - 6x + 8}}{{4x - 1}} \ge 0\) có tập nghiệm là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivaiabg2 % da9maajadabaWaaSaaaeaacaaIXaaabaGaaGinaaaacaGG7aGaamyy % aaGaayjkaiaaw2faaiabgQIiipaajibabaGaamOyaiaacUdacqGHRa % WkcqGHEisPaiaawUfacaGLPaaaaaa!445E! T = \left( {\frac{1}{4};a} \right] \cup \left[ {b; + \infty } \right)\). Hỏi M = a+ b bằng
-
Mặt phẳng đi qua ba điểm A( 0 ; 0 ;2), B( 1 ; 0 ; 0 ) và C( 0 ; 3 ; 0) có phương trình là:
-
Cho a,b,c là các số thực sao cho phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamOEamaaCaaaleqabaGaaG4maaaakiabgUca % RiaadggacaWG6bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOyai % aadQhacqGHRaWkcaWGJbGaeyypa0JaaGimaaaa!48ED! {z^3} + a{z^2} + bz + c = 0\) có ba nghiệm phức lần lượt là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamOEamaaBaaaleaacaaIXaaabeaakiabg2da % 9iabeM8a3jabgUcaRiaaiodacaWGPbGaai4oaiaabccacaWG6bWaaS % baaSqaaiaaikdaaeqaaOGaeyypa0JaeqyYdCNaey4kaSIaaGyoaiaa % dMgacaGG7aGaaeiiaiaadQhadaWgaaWcbaGaaG4maaqabaGccqGH9a % qpcaaIYaGaeqyYdCNaeyOeI0IaaGinaaaa!5585! {z_1} = \omega + 3i;{\rm{ }}{z_2} = \omega + 9i;{\rm{ }}{z_3} = 2\omega - 4\), trong đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaeqyYdChaaa!3EBB! \omega \) là một số phức nào đó. Tính giá trị của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D % aerbdfgBPjMCPbqeeuuDJXwAKbsr4rNCHbGeaGqiVu0Je9sqqrpepC % 0xbbL8F4rqqrFfpeea0xe9Lq-Jc9vqaqpepm0xbba9pwe9Q8fs0-yq % aqpepae9pg0FirpepeKkFr0xfr-xfr-xb9adbaqaaeGaciGaaiaabe % qaamaaeaqbaaGcbaGaamiuaiabg2da9maaemaabaGaamyyaiabgUca % RiaadkgacqGHRaWkcaWGJbaacaGLhWUaayjcSdGaaiOlaaaa!4716! P = \left| {a + b + c} \right|.\)
-
Cho tứ diện ABCD có AB = 3a,AC = 4a ,AD = 5a. Gọi M,N,P lần lượt là trọng tâm các tam giác DAB ,DBC ,DCA . Tính thể tích V của tứ diện DMDMNP khi thể tích tứ diện ABCD đạt giá trị lớn nhất.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp khối chóp SABCD.
-
Cho hai số phức \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOEamaaBa % aaleaacaaIXaaabeaakiabg2da9iaaikdacqGHRaWkcaaIZaGaamyA % aaaa!3C33! {z_1} = 2 + 3i\),\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOEamaaBa % aaleaacaaIYaaabeaakiabg2da9iabgkHiTiaaisdacqGHsislcaaI % 1aGaamyAaaaa!3D30! {z_2} = - 4 - 5i\) . Số phức \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOEaiabg2 % da9iaadQhadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWG6bWaaSba % aSqaaiaaikdaaeqaaaaa!3CB2! z = {z_1} + {z_2}\) là
-
Trong không gian Oxyz, cho hình thoi ABCD với A(-1;2;1) ; B (2;3;2). Tâm I của hình thoi thuộc đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaacQ % dadaWcaaqaaiaadIhacqGHRaWkcaaIXaaabaGaeyOeI0IaaGymaaaa % cqGH9aqpdaWcaaqaaiaadMhaaeaacqGHsislcaaIXaaaaiabg2da9m % aalaaabaGaamOEaiabgkHiTiaaikdaaeaacaaIXaaaaaaa!4421! d:\frac{{x + 1}}{{ - 1}} = \frac{y}{{ - 1}} = \frac{{z - 2}}{1}\). Tọa độ đỉnh D là
-
Nghiệm của phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqaM5cvLHfij5gC1rhimfMBNvxyNvga7TNm951EYG % xlX0xFTWLzYf2y7ftF7HtF9adatCvAUfeBSjuyZL2yd9gzLbvyNv2C % aerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLD % harqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr % 0xc9pk0xbba9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYR % Xxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaaba % aaaaaaaapeGaaGOma8aadaahaaWcbeqaa8qacaaIYaGaamiEaiabgk % HiTiaaigdaaaGccqGHsisldaWcaaWdaeaapeGaaGymaaWdaeaapeGa % aGioaaaacqGH9aqpcaaIWaaaaa!4F78! {2^{2x - 1}} - \frac{1}{8} = 0\) là
-
Số giá trị nguyên của m < 0 để hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iGacYgacaGGUbWaaeWaaeaacaWG4bWaaWbaaSqabeaacaaIYaaa % aOGaey4kaSIaamyBaiaadIhacqGHRaWkcaaIXaaacaGLOaGaayzkaa % aaaa!41C3! y = \ln \left( {{x^2} + mx + 1} \right)\) đồng biến trên \((0;+\infty)\) là
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9 % Ff0dmeGabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWG5bGaeyypa0 % ZaaSaaaeaacaWG4bGaeyOeI0IaaGymaaqaaiaaikdacqGHsislcaWG % 4baaaaaa!3CE1! y = \frac{{x - 1}}{{2 - x}}\).Giá trị nhỏ nhất của hàm số trên đoạn [3;4] là
-
Đồ thị (C) của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqabeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaigdaaeaacaWG4bGaeyOeI0Ia % aGymaaaaaaa!3D48! y = \frac{{x + 1}}{{x - 1}}\) và đường thẳng d; y = 2x -1 cắt nhau tại hai điểm A và B khi đó độ dài đoạn AB bằng?
-
Phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmamaaCa % aaleqabaGaamiEamaaCaaameqabaGaaGOmaaaaliabgkHiTiaaioda % caWG4bGaey4kaSIaaGOmaaaakiabg2da9iaaisdaaaa!3EE2! {2^{{x^2} - 3x + 2}} = 4\) có 2 nghiệm là \(x_1;x_2\) . Hãy tính giá trị của \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivaiabg2 % da9iaadIhadaqhaaWcbaGaaGymaaqaaiaaiodaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaaikdaaeaacaaIZaaaaaaa!3E04! T = x_1^3 + x_2^3\).
-
Trong không gian với hệ tọa độ Oxyz cho đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0l % bbf9q8WrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0R % Yxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGa % caGaaeqabaqaaeaadaaakeaacaWGKbGaaiOoamaalaaabaGaamiEai % abgUcaRiaaiodaaeaacaaIYaaaaiabg2da9maalaaabaGaamyEaiab % gkHiTiaaigdaaeaacaaIXaaaaiabg2da9maalaaabaGaamOEaiabgk % HiTiaaigdaaeaacqGHsislcaaIZaaaaaaa!40A4! d:\frac{{x + 3}}{2} = \frac{{y - 1}}{1} = \frac{{z - 1}}{{ - 3}}\). Hình chiếu vuông góc của d trên mặt phẳng (Oyz) là một đường thẳng có vectơ chỉ phương là
-
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A( -3;1; -4) và B(1; -1;2). Phương trình mặt cầu (S) nhận AB làm đường kính là
