Cho hàm số \(f(x)={{x}^{3}}+a{{x}^{2}}+bx-2\) thỏa mãn \(\left\{ \begin{array}{l}a + b > 1\\3 + 2a + b < 0\end{array} \right.\). Số điểm cực trị của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(f\left( x \right) = {x^3} + a{x^2} + bx - 2\) có \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \), \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \).
Ta có:
\(\begin{array}{l}f\left( 1 \right) = 1 + a + b - 2 = a + b - 1 > 0\\f\left( 2 \right) = 8 + 4a + 2b - 2 = 2\left( {2a + b - 3} \right) < 0\end{array}\)
Do đó phương trình \(f\left( x \right) = 0\) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} \in \left( {0;1} \right)\\{x_2} \in \left( {1;2} \right)\\{x_3} \in \left( {2; + \infty } \right)\end{array} \right.\).
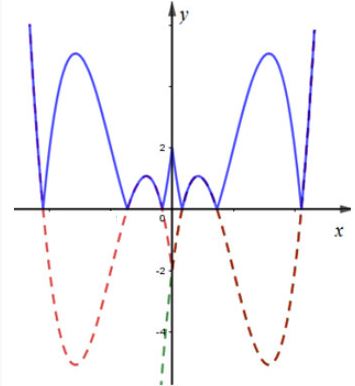
Ta có đồ thị hàm số \(y=\left| f\left( \left| x \right| \right) \right|\) như sau:
Như vậy, hàm số \(y=\left| f\left( \left| x \right| \right) \right|\) có tất cả 11 cực trị.
Chọn D.
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Thị Diệu