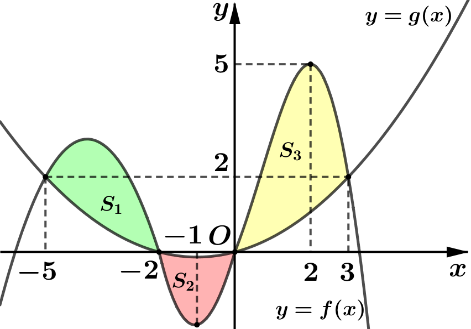
Cho hàm số \(f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)\) có đồ thị là đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right):y=g\left( x \right)\) tiếp xúc với \(\left( C \right)\) tại điểm \({{x}_{0}}=1\). Biết \(\left( d \right)\) và \(\left( C \right)\) còn hai điểm chung khác có hoành độ là \({{x}_{1}},{{x}_{2}}\left( {{x}_{1}}<{{x}_{2}} \right)\) và \(\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{g\left( x \right)-f\left( x \right)}{{{\left( x-1 \right)}^{2}}}dx=\frac{4}{3}}\). Tính diện tích hình phẳng giới hạn bởi đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right)\).

A. \(\frac{29}{5}\).

B. \(\frac{28}{5}\).

C. \(\frac{143}{5}\).

D. \(\frac{43}{5}\).

Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Chủ đề: Đề thi THPT QG

Môn: Toán

Lời giải:

Báo sai

Chọn A

Theo giả thiết ta có: \(f\left( x \right)-g\left( x \right)\)\( ={{\left( x-1 \right)}^{2}}\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\)\( ={{x}^{4}}+b{{x}^{2}}-mx+n\,\,\left( * \right)\)

Ta có: \(\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{f\left( x \right)-g\left( x \right)}{{{\left( x-1 \right)}^{2}}}dx}\)\(=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)dx}\)\(=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left( x-{{x}_{1}} \right)\left( x-{{x}_{1}}+{{x}_{1}}-{{x}_{2}} \right)dx}\)

\(\begin{align} & =\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\left[ {{\left( x-{{x}_{1}} \right)}^{2}}+\left( x-{{x}_{1}} \right)\left( {{x}_{1}}-{{x}_{2}} \right) \right]dx}\\ &=\left. \left( \frac{{{\left( x-{{x}_{1}} \right)}^{3}}}{3}+\left( {{x}_{1}}-{{x}_{2}} \right)\frac{{{\left( x-{{x}_{1}} \right)}^{2}}}{2} \right) \right|_{{{x}_{1}}}^{{{x}_{2}}} \\ & =\frac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{3}-\frac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{2}\\ &=-\frac{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}}{6}=\frac{-4}{3} \\ \end{align}\)

Suy ra \({{\left( {{x}_{2}}-{{x}_{1}} \right)}^{3}}=8\Leftrightarrow {{x}_{2}}-{{x}_{1}}=2\,\,\,\,\,\,\,\left( 1 \right)\)

Mặt khác theo định lí Viét bậc 4 của phương trình (*) ta được:

\(1+1+{{x}_{2}}+{{x}_{1}}=0\Leftrightarrow {{x}_{2}}+{{x}_{1}}=-2\,\left( 2 \right)\)

Từ \(\left( 1 \right),\left( 2 \right)\)

\(\Rightarrow \left\{ \begin{align} & {{x}_{2}}=0 \\ & {{x}_{1}}=-2 \\ \end{align} \right.\)

Vậy diện tích hình phẳng giới hạn bởi đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right)\)là:

\(S=\int\limits_{-2}^{1}{\left| {{\left( x-1 \right)}^{2}}\left( x+2 \right)x \right|}dx\)\( =\frac{29}{5}\)

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài