Đồ thị hàm số y = ∣x3∣−3x2 + 1 có bao nhiêu điểm cực trị?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hàm số y = x3 − 3x2 + 1
Tập xác định: D = R
Đạo hàm \(y\prime = 3{x^2} - 6x;y\prime = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 2
\end{array} \right.\)
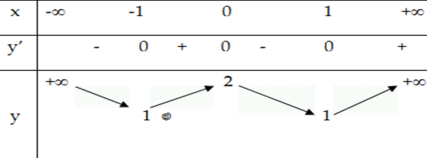
Bảng biến thiên:
.png)
Hàm số \(y = \mid {x^3}\mid - 3{x^2} + 1 = \left\{ \begin{array}{l}
{x^3} - 3{x^2} + 1,x \ge 0\\
- {x^3} - 3{x^2} + 1,x < 0
\end{array} \right.\) là hàm số chẵn và đồ thị của nó được suy ra từ đồ thị hàm số y=x3−3x2+1 bằng cách bỏ đi phần bên trái trục tung. Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải Oy qua Oy.
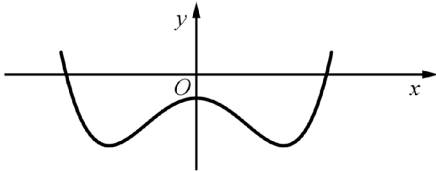
Như vậy ta sẽ được đồ thị hàm số y=∣x3∣−3x2+1 có dạng như sau:
.png)
Vậy đồ thị hàm số y = ∣x3∣−3x2 + 1 có ba điểm cực trị.



.png)