Cho hàm số f có đạo hàm là \(f'\left( x \right) = x{(x + 1)^2}{(x - 2)^4}\) với mọi x ∈ R. Số điểm cực trị của hàm số f là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có
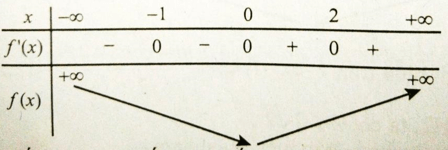
\(f'\left( x \right) = 0 \Leftrightarrow x{\left( {x + 1} \right)^2}{\left( {x - 2} \right)^2} = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = - 1\\
x = 2
\end{array} \right.\)
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại x = 0. Vậy hàm số có một cực trị.
Câu hỏi liên quan
-
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f’\left( x \right)\) là đường cong ở hình bên. Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị ?
.jpg.png)
-
Cho hàm số \(y = 3{x^4} - 4{x^3} + 2\). Khẳng định nào sau đây là đúng
-
Hàm số \(y = \frac{1}{3}{x^3} + {x^2} - \frac{2}{3}\) có
-
Cho hàm số \(y = \sqrt 2 {x^4} – \frac{1}{{\sqrt 3 }}{x^2} + 3\). Số điểm cực trị của hàm số là.
-
Số điểm cực đại của hàm số \(f\left( x \right) = \frac{1}{3}{{\rm{x}}^4} + {{\rm{x}}^2} + 7\) là
-
Cho hàm số y = x4-2mx2+2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có ba điểm cực trị A; B; C thỏa mãn OA.OB.OC = 12?
-
Tìm tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(2 m-1) x-3\) có cực trị
-
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
-
Tìm số điểm cực trị của hàm số \(y = {x^4} + 3{x^2} – 3\)?
-
Đồ thị hàm số \(y = {\left| x \right|^3} - 3{x^2} - 1\) có bao nhiêu điểm cực trị?
-
Cho hàm số \(y=(m-1) x^{4}-3 m x^{2}+5\) . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
-
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = x⁸ + (m -1)x⁵ - (m² -1)x⁴ +1 \) đạt cực tiểu taị x=0
-
Hiệu số giữa giá trị cực đại và giá trị cực tiểu của hàm số \(y = {x^3} - 3{x^2} + 4\) là
-
Cho hàm số \(y = - \frac{1}{3}{x^3} + 4{x^2} - 5x - 17\). Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là x1, x2. Khi đó, tích số có giá trị là
-
Điểm cực trị của đồ thị hàm số \(y=\sqrt{1+4 x-x^{4}}\) có tọa độ là:
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = 3{{\rm{x}}^4}{\rm{ - 5}}{{\rm{x}}^2} - 3\) là
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = \frac{1}{3}{{\rm{x}}^4} + {{\rm{x}}^2} + 7\) là
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = - 5{{\rm{x}}^4}{\rm{ + }}{{\rm{x}}^2} + 7\) là
-
Tìm m để hàm số \(y = x³ - 2mx² + mx + 1 \) đạt cực tiểu tại x=1
-
Số cực trị của hàm số \(f\left( x \right) = - 5{{\rm{x}}^4} - 2{{\rm{x}}^2} + 3\) là
