Cho hàm số y=f(x) có đồ thị hàm số y=f′(x) như hình vẽ. Hỏi hàm số y=f(3x–5) có bao nhiêu điểm cực tiểu?
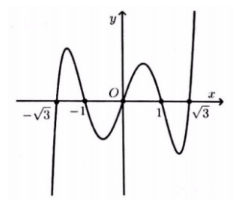
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(y=f(3x-5)\Rightarrow y'=3f'(3x-5)\)
Khi đó
\(\begin{array}{l} y' > 0 \Leftrightarrow 3f'(3x - 5) > 0\\ \Leftrightarrow \left[ \begin{array}{l} - \sqrt 3 < 3x - 5 < - 1\\ 0 < 3x - 5 < 1\\ \sqrt 3 < 3x - 5 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \frac{{5 - \sqrt 3 }}{3} < x < \frac{4}{3}\\ \frac{5}{3} < x < 2\\ \frac{{\sqrt 3 + 5}}{3} < x \end{array} \right.\\ \end{array}\)
Tương tự ta có:
\(y' > 0 \Leftrightarrow \left[ \begin{array}{l} x < \frac{{5 - \sqrt 3 }}{3}\\ \frac{4}{3} < x < \frac{5}{3}\\ 2 < x < \frac{{\sqrt 3 + 5}}{3} \end{array} \right.\)
Bảng xét dấu y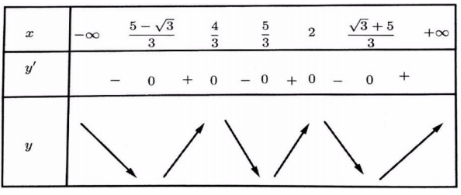
Dựa vào bảng xét dấu suy ra hàm số y=f(3x-5) có 3 điểm cực tiểu.



.png)
.jpg.png)
.jpg.png)











