ADMICRO
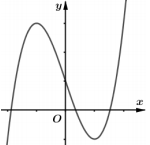
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và đồ thị hình bên dưới là đồ thị của đạo hàm f'(x) . Hàm số \(g(x)=f(|x|)+2018\) có bao nhiêu điểm cực trị ?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
Bài: Cực trị của hàm số
ZUNIA12
Lời giải:
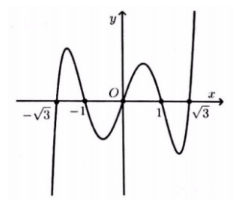
Báo saiTừ đồ thị hàm số y=f'(x) ta thấy f'(x) cắt trục hoành tại 2 điểm có hoành độ dương (và 1 điểm có hoành độ âm)
\(\Rightarrow \) f(x) có 2 điểm cực trị dương
\(\Rightarrow f(|x|)\) có 5 điểm cực trị
\(\Rightarrow g(x)=f(|x|)+2018\) có 5 điểm cực trị (vì tịnh tiến lên trên hay xuống dưới không ảnh hưởng đến số điểm cực trị của hàm số)
ZUNIA9
AANETWORK



.png)











