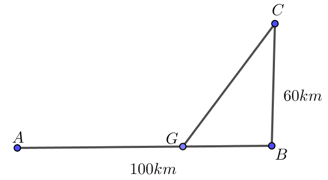
Cho hàm số \( y = mx⁴ + (2m +1)x² +1\). Tìm tất cả các giá trị thực của tham số m để hàm số có đúng một điểm cực tiểu.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiVới m = 0, ta có \( y = x² +1 \Rightarrow y ' = 2 x\) . Khi đó hàm số có 1 cực trị và cực trị đó là cực tiểu.
Suy ra m = 0 thỏa mãn yêu cầu bài toán. (1)
Với \(m \ne 0\) , ta có \(y ' = 4mx³ + 2(2m +1)x = 2x(2mx² + 2m +1)\)
Hàm số có một cực trị là cực tiểu \(\left\{ \begin{array}{l} m > 0\\ 2m{x^2} + 2m + 1 = 0\,\,\,\rm{vô\,nghiệm} \end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l} m > 0\\ \frac{{ - 2m - 1}}{{2m}} = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m > 0\\ \left[ \begin{array}{l} m < \frac{{ - 1}}{2}\\ m > 0 \end{array} \right. \end{array} \right. \Leftrightarrow m > 0\,\,\,\,(2)\)
Từ (1) và (2) suy ra hàm số có một cực tiểu khi và chỉ khi \(m\ge0\)



.png)