Cho hàm số bậc ba \(f(x)=a x^{3}+b x^{2}+c x+d\) có đồ thị như hình vẽ bên dưới:
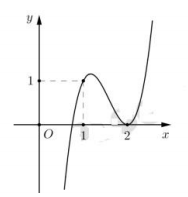
Hỏi đồ thị hàm số \(g(x)=\frac{\left(x^{2}-3 x+2\right) \sqrt{x-1}}{(x+1)\left[f^{2}(x)-f(x)\right]}\) có bao nhiêu đường tiệm cận đứng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐK: \(x \geq \frac{1}{2} ; f(x) \neq 0 ; f(x) \neq 1\)
Số tiệm cận đứng của y=g(x) tương ứng số số nghiệm của phương trình
\((x+1)\left[f^{2}(x)-f(x)\right]=0 \Leftrightarrow\left[\begin{array}{l} x=-1(l) \\ f^{2}(x)-f(x)=0 \end{array} \Leftrightarrow\left[\begin{array}{l} x=-1(l) \\ f(x)=1(1) \\ f(x)=0(2) \end{array}\right.\right.\)
+ Xét phương trình (1) , theo hình vẽ ta thấy phương trình sẽ có 3 nghiệm:
\(\left[\begin{array}{l} x_{1}=1(l) \\ 1<x_{2}<2(t m)=> \\ 2<x_{3}<2(t m) \end{array}\right.\)có 2 tiệm cận đứng.
+ Xét phương trình (2) f(x)=0 , theo hình vẽ ta thấy phương trình sẽ có 2 nghiệm
\(\left[\begin{array}{l} x_{4}=a(a<1)(l) \\ x_{5}=2(t m) \end{array}\right.\)
Do nghiệm \(x_5=2\) là nghiệm kép và trên tử là nghiệm đơn nên \(x_5=2\) vẫn là một tiệm cận đứng \(\Rightarrow \) có 1 tiệm cận đứng
Vậy tổng cộng g (x) có tất cả 3 tiệm cận đứng















