Đề thi HK1 môn Toán 10 KNTT năm 2022-2023
Trường THPT Nguyễn Khuyến
-
Câu 1:
Trong các câu sau, câu nào là mệnh đề?
A. 6+x=4x2.6+x=4x2.
B. a<2.
C. 123 là số nguyên tố phải không?
D. Bắc Giang là tỉnh thuộc miền Nam Việt Nam.
-
Câu 2:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. ∅={0}.
B. ∅⊂{0}.
C. {0}⊂∅.
D. 0⊂∅.
-
Câu 3:
Phủ định của mệnh đề “5+8=13” là mệnh đề
A. 5+8<13.
B. 5+8≥13.
C. 5+8>13.
D. 5+8≠13.
-
Câu 4:
Mệnh đề nào sau đây đúng?
A. Nếu a là số tự nhiên thì a là số hữu tỉ không âm.
B. Nếu a là số hữu tỉ không âm thì a là số tự nhiên.
C. Nếu a là số hữu tỉ dương thì a là số tự nhiên.
D. Nếu a không là số tự nhiên thì a không phải là số hữu tỉ không âm.
-
Câu 5:
Cho x là một phần tử của tập hợp X. Xét các mệnh đề sau:
(I)x∈X;
(II){x}∈X;
(III)x⊂X;
(IV){x}⊂X.
Trong các mệnh đề trên, mệnh đề nào đúng?
A. (I) và (II)
B. (I) và (III)
C. (I) và (IV)
D. (II) và (IV)
-
Câu 6:
Cho ba tập hợp sau:
E={x∈R|f(x)=0};F={x∈R|g(x)=0};H={x∈R|f(x)g(x)=0}.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. H=E∩F.
B. H=E∪F.
C. H=E∖F.
D. H=F∖E.
-
Câu 7:
Cho hai tập hợp X={n∈N|n là bội của 2 và 3}, Y={n∈N|n là bội của 6}. Trong các mệnh đề sau, mệnh đề nào sai?
A. Y⊂X.
B. X⊂Y.
C. ∃n:n∈X và n∉Y.
D. X=Y.
-
Câu 8:
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 2x2+3y>4.
B. xy+x<5.
C. 32x+43y≥6.
D. x+y3≤3.
-
Câu 9:
Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
A. {2x+3y>423x+3y2<1.
B. {x+y>423x+32y<1.
C. {x>3y<2x+y≥y2.
D. {x−y≤3y<1x+y≥x+xy.
-
Câu 10:
Điểm nào sau đây thuộc miền nghiệm của bất phương trình 2x+5y≤10?
A. (5;2).
B. (−1;4).
C. (2;1).
D. (−5;6).
-
Câu 11:
Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x−3y>13?
A. (1;−5).
B. (2;−4).
C. (3;−3).
D. (8;1).
-
Câu 12:
Cho bất phương trình x+2y≤3. Khẳng định nào sau đây là đúng?
A. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d:x+2y=3 chứa gốc tọa độ.
B. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d:x+2y=3 không chứa gốc tọa độ.
C. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d:x+2y=−3 chứa gốc tọa độ.
D. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d:x+2y=−3 không chứa gốc tọa độ.
-
Câu 13:
Cặp số nào dưới đây là nghiệm của hệ bất phương trình {x+y≤2x−2y≥4x>0?
A. (−1;2).
B. (−2;−4).
C. (0;1).
D. (2;4).
-
Câu 14:
Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình {−x+y≤2x−2y≥1y≤0?
A. (−3;2).
B. (0;1).
C. (4;−1).
D. (−2;2).
-
Câu 15:
Tam giác ABC có ˆA=15∘,ˆB=45∘. Giá trị của tanC bằng:
A. −√3.
B. √3.
C. 1√3.
D. −1√3.
-
Câu 16:
Trên mặt phẳng tọa độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho ^xOM=135∘. Tích hoành độ và tung độ của điểm M bằng
A. 12√2
B. 12
C. −12
D. −12√2
-
Câu 17:
Trên mặt phẳng tọa độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho ^xOM=150∘. N là điểm đối xứng với M qua trục tung. Giá trị của tan^xON bằng:
.png)
A. 1√3.
B. −1√3.
C. √3.
D. −√3.
-
Câu 18:
Cho góc nhọn α có tanα=34. Giá trị của sinα.cosα bằng
A. 43.
B. 1225.
C. 2512.
D. 34.
-
Câu 19:
Cho góc nhọn α(0∘<α<180∘) thỏa mãn sinα+cosα=1. Giá trị của cotα bằng:
A. 0.
B. 1.
C. −1.
D. Không tồn tại
-
Câu 20:
Cho góc α thỏa mãn sinα+cosα=√2. Giá trị của tanα+cotα là:
A. 1.
B. −2.
C. 0.
D. 2.
-
Câu 21:
Số quy tròn của số gần đúng 167,23±0,07 là:
A. 167,23
B. 167,2
C. 167,3
D. 167
-
Câu 22:
Biết độ ẩm không khí tại Hà Nội là: 51%±2%. Khi đó
A. Sai số tuyệt đối δ=2%
B. Sai số tuyệt đối δ=1%
C. Độ chính xác d=2%
D. Độ chính xác d=1%
-
Câu 23:
Một học sinh thực hành đo chiều cao của một tòa tháp cho kết quả là 200 m. Biết chiều cao thực của tòa tháp là 201 m, sai số tương đối là:
A. 0,5%
B. 1%
C. 2%
D. 4%
-
Câu 24:
Cho hình bình hành ABCD tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm A,B,C,D và O. Số các vectơ khác vectơ – không và cùng phương với →AC là:
A. 6
B. 3
C. 4
D. 2
-
Câu 25:
Cho đoạn thẳng AC và B là một điểm nằm giữa A,C. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
A. Hai vectơ →AB và →CB cùng hướng.
B. Hai vectơ →CA và →BC cùng hướng.
C. Hai vectơ →AB và →AC cùng hướng.
D. Hai vectơ →AC và →BA cùng hướng.
-
Câu 26:
Cho hình bình hành ABCD tâm O. Gọi K,L,M,N tướng ứng là trung điểm các cạnh AB,BC,CD,DA. Trong các vectơ có đầu mút lấy từ các điểm A,B,C,D,K,L,M,O có bao nhiêu vectơ bằng vectơ →AK ?
A. 2
B. 6
C. 4
D. 8
-
Câu 27:
Cho hình thoi ABCD có độ dài các cạnh bằng 1 và ^DAB=120∘. Khẳng định nào sau đây là đúng?
A. →AB=→CD
B. →BD=→AC
C. |→BD|=1
D. |→AC|=1
-
Câu 28:
Một học sinh thực hành đo chiều cao của một tòa tháp cho kết quả là 200 m. Biết chiều cao thực của tòa tháp là 201 m, sai số tương đối là:
A. 0,5%
B. 1%
C. 2%
D. 4%
-
Câu 29:
Điểm thi học kỳ môn Toán của một nhóm bạn như sau:
8
9
7
10
7
5
7
8
Mốt của mấu số liệu trên là:
A. 5
B. 7
C. 8
D. 9
-
Câu 30:
Điểm thi học kỳ môn Toán của một nhóm bạn như sau:
8
9
7
10
7
5
7
8
Trung vị của mẫu số liệu là:
A. 6
B. 7
C. 7.5
D. 8
-
Câu 31:
Trên mặt phẳng tọa độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị, sao cho cos^xOM=−35. (H.3.4). Diện tích của tam giác AOM bằng:
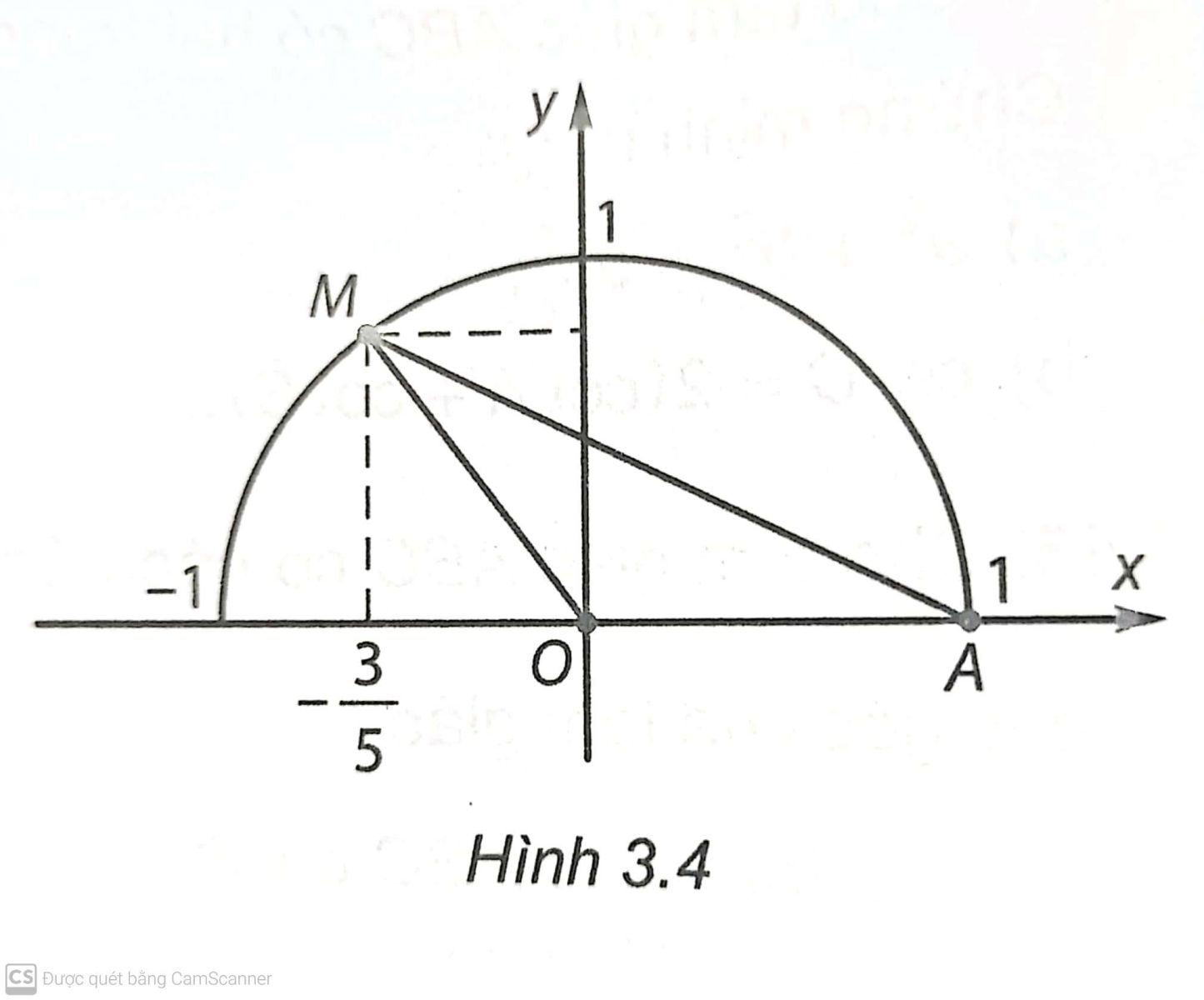
A. 45.
B. 25.
C. 35.
D. 310.
-
Câu 32:
Trên mặt phẳng tọa độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho ^xOM=150∘(H.3.5). N là điểm đối xứng với M qua trục tung. Diện tích của tam giác MAN bằng:
A. √34.
B. √32.
C. √3.
D. 2√3.
-
Câu 33:
Cho tam giác ABC đều, trọng tâm G, có độ dài các cạnh bằng 3. Độ dài vectơ →AG bằng
A. √3
B. 3√32
C. √32
D. 2√3
-
Câu 34:
Cho tam giác ABC vuông tại A và AB=3,AC=4. Độ dài của vectơ →CB+→AB bằng
A. √13
B. 2√13
C. 4
D. 2
-
Câu 35:
Cho tam giác ABC có AB=2,BC=4 và ^ABC=60∘. Độ dài của vectơ →AC−→BA bằng
A. 2
B. √19
C. 4
D. √192
-
Câu 36:
Cho tam giác ABC và điểm I sao cho →IB+2→IC=→0. Khẳng định nào sau đây là một khẳng định đúng?
A. →AI=2→AC−→AB
B. →AI=→AB−2→AC
C. →AI=→AB−2→AC−3
D. →AI=→AB+2→AC3
-
Câu 37:
Cho cosα=14. Giá trị của P=tanα+2cotα2tanα+3cotα là:
A. −1733.
B. 1733.
C. 12.
D. 1633.
-
Câu 38:
Tam giác ABC có a=2,b=3,c=4. Bán kính đường tròn ngoại tiếp của tam giác ABC là:
A. R=√152.
B. R=7√15.
C. R=√156.
D. R=8√15.
-
Câu 39:
Gọi G là trọng tâm của tam giác ABC và M là trung điểm cạnh BC. Khẳng định nào sau đây là một khẳng định đúng?
A. →GA=2→GM
B. →AB+→AC=3→AG
C. →AM=3→MG
D. 3→GA=2→AM
-
Câu 40:
Trong mặt phẳng tọa độ Oxy cho ba điểm A(−3;1),B(2;−1),C(4;6). Trọng tâm G của tam giác ABC có tọa độ là:
A. (1;2)
B. (2;1)
C. (1;−2)
D. (−2;1)














