Cho tam giác ABC cân tại A. Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB theo thứ tự lập thành cấp số nhân với công bội q. Khẳng định nào dưới đây đúng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai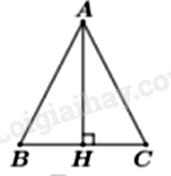
Vì BC, AH, AB theo thứ tự lập thành cấp số nhân nên ta có: \(AH = BC.q,AB = AH.q = BC.{q^2}\), suy ra \(\left\{ \begin{array}{l}A{H^2} = BC.AB\\\frac{{AB}}{{BC}} = {q^2}\end{array} \right.\)
Vì tam giác ABC cân tại A nên AH là đường cao đồng thời là đường trung tuyến nên \(BH = \frac{{BC}}{2}\)
Áp định lí Pythagore vào tam giác ABH vuông tại H có:
\(A{H^2} = A{B^2} - B{H^2} = A{B^2} - \frac{{B{C^2}}}{4} \Rightarrow 4{\left( {\frac{{AB}}{{BC}}} \right)^2} - 4\frac{{AB}}{{BC}} - 1 = 0\)
\( \Rightarrow \frac{{AB}}{{BC}} = \frac{{\sqrt 2 + 1}}{2}\) (do \(\frac{{AB}}{{BC}} > 0\))
Vậy \({q^2} = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 + 1}}{2}\)
Đáp án A
Đề thi giữa HK1 môn Toán 11 CD năm 2023-2024
Trường THPT Trần Nhân Tông















