500 câu trắc nghiệm giữa HK1 Toán 8 - CTST - Đề 2
18 câu hỏi 60 phút
Trong các biểu thức sau, biểu thức nào là đơn thức thu gọn?
\( - {x^4}{y^3}x.\)
\(\frac{1}{3}{x^4}{y^3}.\)
\(\frac{1}{3}{x^2}{y^2}yz.\)
\(\frac{{ - 1}}{3}x{y^4}zxy.\)
Vì đơn thức \(\frac{1}{3}{x^4}{y^3}\) có dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương nên đơn thức \(\frac{1}{3}{x^4}{y^3}\) là đơn thức thu gọn.
Danh sách câu hỏi:
Vì đơn thức \(\frac{1}{3}{x^4}{y^3}\) có dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương nên đơn thức \(\frac{1}{3}{x^4}{y^3}\) là đơn thức thu gọn.
Đơn thức \(30{x^2}{y^3}\) chia hết cho đơn thức \(60xy\) (vì số mũ ở mỗi biến của đơn thức \(30{x^2}{y^3}\) đều lớn hơn số mũ ở mỗi biến của đơn thức \(60xy\)).
Đẳng thức \(a\left( {a + 1} \right) = {a^2} + a\) là hằng đẳng thức.
Các đẳng thức \(3a + 1 = a + 3\); \(a + 3 = 3a - 1\); \(2\left( {a - 2} \right) = 4a\) không phải là hằng đẳng thức (vì khi ta thay \(a = 0\) thì hai vế của mỗi đẳng thức không bằng nhau).
Với điều kiện phân thức có nghĩa, ta có \(\frac{{ - 2xy}}{{6{x^3}{y^2}}} = \frac{{2xy \cdot \left( { - 1} \right)}}{{2xy \cdot 3{x^2}y}} = \frac{{ - 1}}{{3{x^2}y}}.\)
Nếu hình chóp có đáy là tam giác đều, chân đường cao trùng với trọng tâm của tam giác thì nó là hình chóp đều.
Câu 10:
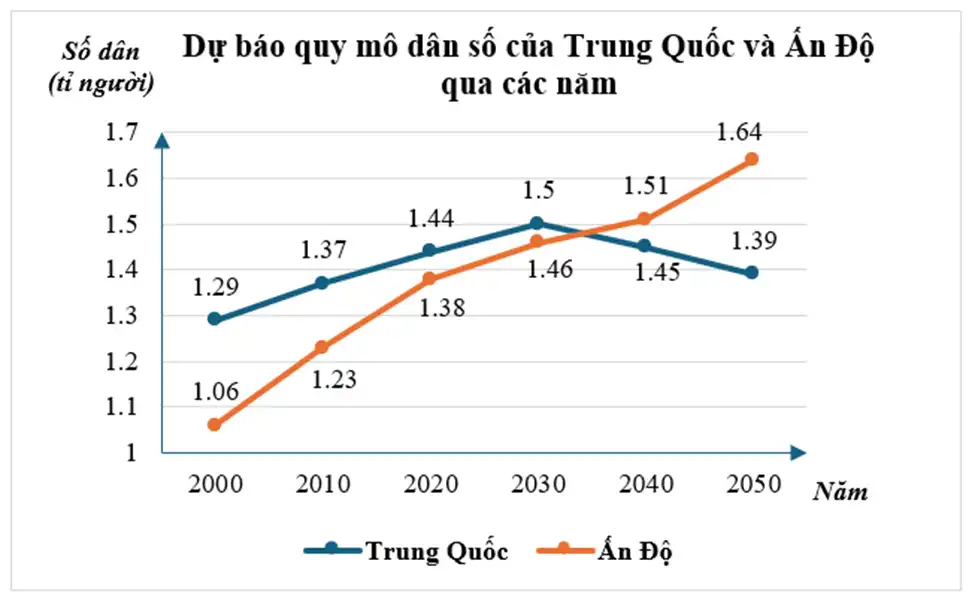
Khi muốn biểu diễn tuổi thọ trung bình của người Việt Nam qua 40 năm. Ta nên lựa chọn biểu đồ nào?
Câu 13:
Cho hai đa thức: \(A = 2xy\left( {x{y^2} - 3{x^2}y + 1} \right)\) và \(B = \left( {12{x^4}{y^5} - 36{x^5}{y^4} + 6{x^3}{y^3}} \right):6{x^2}{y^2}.\)
Đa thức \(M\) thỏa mãn \(A = M + B.\)
Bậc của đa thức \(A\) là 5
Hệ số tự do của đa thức \(B\) là 2
Giá trị của biểu thức \(B\) tại \(x = - 1\,;\,\,y = 1\) là 12
\(M\) là một đơn thức
Câu 14:
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC,\) đường cao \(AH.\) Từ \(H\) kẻ \(HM \bot AB\,\left( {M \in AB} \right).\) Kẻ \(HN \bot AC\,\left( {N \in AC} \right).\) Trên tia đối của tia \(MH\) lấy điểm \(P\) sao cho \(M\) là trung điểm của \(PH.\) Gọi \(I\) là trung điểm của \(HC,\) lấy \(K\) trên tia \(AI\) sao cho \(I\) là trung điểm của \(AK;\,MN\) cắt \(AH\) tại \(O,\) \(CO\) cắt \(AK\) tại \(D.\)
\(\widehat {HKC} = \frac{1}{2}\widehat {HAC}\)
Tứ giác \(AMHN\) là hình chữ nhật
Tứ giác \(MNCK\) là hình thang vuông
\(AK = 2AD\)