Một vật dao động theo phương trình \( x = 20\cos \left( {\frac{{5\pi }}{3}t - \frac{\pi }{6}} \right){\mkern 1mu} {\mkern 1mu} cm\). Kể từ lúc t = 0 đến lúc vật đi qua vị trí x = - 10 cm theo chiều âm lần thứ 2015 thì lực hồi phục sinh công dương trong thời gian
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChu kì của dao động: \( T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{5\pi }}{3}}} = 1,2{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Nhận xét: lực hồi phục sinh công dương, nên công suất của lực hồi phục P=Fph.v>0→ lực hồi phục và vận tốc cùng dấu, khi vật hướng về VTCB. → Trong 1 chu kì, lực hồi phục sinh công dương trong thời gian T2
Pha ban đầu của dao động: \( \varphi = - \frac{\pi }{6}{\mkern 1mu} {\mkern 1mu} \left( {rad} \right)\)
Trong 1 chu kì, vật qua vị trí x = - 10 cm theo chiều âm 1 lần.
Ta có: 2015 = 2014 + 1
Thời gian lực phục hồi sinh công dương từ lúc t = 0 đến lúc vật đi qua vị trí x = - 10 cm theo chiều âm lần thứ 2015 là \( 2014.\frac{T}{2}\) và thời gian lực phục hồi sinh công dương từ lúc t = 0 đến lúc vật qua vị trí x = - 10 cm theo chiều âm lần đầu tiên.
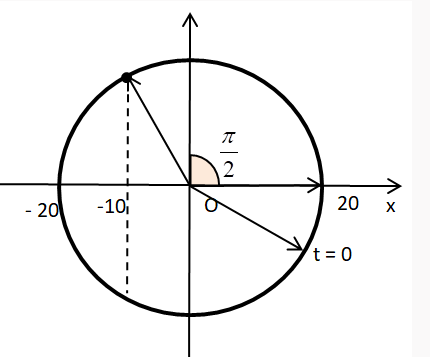
Ta có vòng tròn lượng giác:
Từ VTLG, ta thấy từ lúc t = 0 đến lúc vật qua vị trí x = - 10 cm theo chiều âm lần đầu tiên, lực hồi phục sinh công dương ứng với thời gian vật đi từ vị trí biên dương đến VTCB:
\(t= \frac{{{\rm{\Delta }}\varphi }}{\omega } = \frac{{{\rm{\Delta }}\varphi }}{{\frac{{2\pi }}{T}}} = \frac{{\frac{\pi }{2}}}{{\frac{{2\pi }}{T}}} = \frac{T}{4}\)
Vậy thời gian cần tìm là:
\(2014.\frac{T}{2} + \frac{T}{4} = \frac{{4029}}{4}T = \frac{{4029}}{4}.1,2 = 1208,7{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Chọn B.
