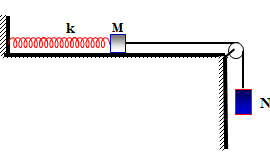
Một vật có khối lượng M = 250 g, đang cân bằng khi treo dưới một lò xo có độ cứng k = 50 N/m. Người ta đặt nhẹ nhàng lên vật M một vật có khối lượng m thì cả hai bắt đầu dao động điều hòa trên phương thẳng đứng và khi cách vị trí ban đầu 2 cm thì chúng có tốc độ 40 cm/s. Khối lượng m bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.PNG)
Ban đầu vật cân bằng ở O, lúc này lò xo giãn:
\(\Delta l = \frac{{{\rm{Mg}}}}{{\rm{k}}} = {\rm{0,05 m}} = {\rm{5 cm}}\)
O’ là VTCB của hệ (M+m):
\(\Delta l' = \frac{{\left( {{\rm{M}} + {\rm{m}}} \right){\rm{g}}}}{{\rm{k}}}\)
Khi đặt vật m nhẹ nhàng lên M, biên độ dao động của hệ lúc này là:
\(\begin{array}{l}
{\rm{A}} = {\rm{OO'}} = \Delta l' - \Delta l\\
{\rm{ }} = \frac{{\left( {{\rm{0,25}} + {\rm{m}}} \right).10}}{{50}} - 0,05 = \frac{{\rm{m}}}{{\rm{5}}}\;\;({\rm{m)}}{\rm{.}}
\end{array}\)
Trong quá trình dao động, bảo toàn cơ năng cho hai vị trí O và M:
\(\begin{array}{l}
{{\rm{W}}_{\rm{O}}} = {{\rm{W}}_{\rm{M}}}\;{\rm{ }}\\
\Leftrightarrow {\rm{ }}\;\frac{1}{2}{\rm{k}}{{\rm{A}}^{\rm{2}}} = \frac{1}{2}\left( {{\rm{M}} + {\rm{m}}} \right){\rm{v}}_{\rm{M}}^{\rm{2}} + \frac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{\left( {{\rm{O'M}}} \right)^{\rm{2}}}
\end{array}\)
(với \({\rm{O'M}} = {\rm{A}} - {\rm{OM}} = \frac{{{\rm{m}} - 0,1}}{5}\quad \left( {\rm{m}} \right)\))
Khi đó:
\(\frac{1}{2}.50.{\left( {\frac{{\rm{m}}}{{\rm{5}}}} \right)^2} = \frac{1}{2}\left( {0,25 + {\rm{m}}} \right)0,{4^2} + \frac{1}{2}.50.{\left( {\frac{{{\rm{m}} - 0,1}}{5}} \right)^2}\)
Suy ra: \({\rm{m}} = 0,25{\rm{ kg}} = 250{\rm{ g}}.\)
Chọn đáp án D
Câu hỏi liên quan
-
Con lắc lò xo ngang dao động điều hoà, vận tốc của vật bằng không khi vật chuyển động qua
-
Tìm câu sai? Biên độ của một con lắc lò xo thẳng đứng dao động điều hoà bằng
-
Con lắc lò xo dao động điều hòa. Khi tăng khối lượng của vật lên 4 lần thì tần số dao động của vật.
-
Con lắc lò xo gồm vật khối lượng m và lò xo có độ cứng k, dao động điều hoà với chu kỳ
-
Con lắc lò xo đang dao động điều hoà trên mặt ngang. Kết luận nào sau đây là sai?
-
Một vật dao động điều hòa trên trục Ox với biên độ 25 cm và tần số f. Thời gian ngắn nhất để vận tốc của vật có giá trị từ - 7π cm/s đến 24π cm/s là 1/4f. Lấy π2 = 10. Gia tốc cực đại của vật trong quá trình dao động là:
-
Một con lắc lò xo gồm một vật nhỏ khối lượng m và lò xo nhẹ có độ cứng k dao động điều hòa với biên độ không đổi là A. Khi con lắc này dao động điều hòa tự do theo phương thẳng đứng thì ở vị trí lò xo có chiều dài tự nhiên, vật có tốc độ bằng 0. Khi con lắc này dao động điều hòa tự do trên mặt phẳng nghiêng góc 300 so với phương ngang thì ở vị trí lò xo có chiều dài tự nhiên, vật có tốc độ bằng v. Nếu con lắc này dao động điều hòa tự do theo phương ngang thì ở vị trí lò xo có chiều dài tự nhiên, vật có tốc độ bằng
-
Một con lắc lò xo khi gắn vật m với lò xo thì chu kì là \(T_1\)= 3s. Nếu gắn vật m đó vào lò xo thì dao động với chu kì \(T_2\)= 4s. Tm chu kì của con lắc lò xo ứng với các trường hợp ghép nối tiếp hai lò xo với nhau
-
Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định gắn chung tại điểm Q. Con lắc (I) nằm ngang trên mặt bàn nhẵn. Con lắc (II) treo thẳng đứng cạnh mép bàn như hình vẽ. Kích thích cho hai con lắc dao động điều hòa tự do. Chọn mốc thế năng đàn hồi của mỗi con lắc tại các vị trí tương ứng của vật lúc lò xo có chiều dài tự nhiên. Thế năng đàn hồi các con lắc phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ. Biết tại thời điểm t = 0, cả hai lò xo đều dãn và \( {t_2} - {t_1} = \frac{\pi }{{12}}s\). Lấy g = 10 m/s2. Tại thời điểm \(t= \frac{\pi }{{10}}{\mkern 1mu} s\), khoảng cách hai vật dao động gần nhất với giá trị nào sau đây ?
-
Hai lò xo L1, L2 có độ cứng k1=40 N/m và k2= 60N/m . Xác định độ cứng của một lò xo tương đương với hai lò xo trên trong trường hợp mắc chúng nối tiếp
-
Một vật nhỏ dao động điều hòa trên trục Ox theo phương trình x = Acos (ωt + φ). Vận tốc của vật có biểu thức là:
-
Một con lắc lò xo gồm lò xo độ cứng k và vật có khối lượng m dao động điều hòa với chu kì T. Chọn câu sai.
-
Một vật dao động điều hòa với phương trình dạng cos. Chọn gốc tính thời gian khi vật đổi chiều chuyển động và khi đó gia tốc của vật đang có giá trị dương. Pha ban đầu là:
-
Hai lò xo có độ cứng \(K_1=23 N/m;K_2=32N/m\); Độ cứng của lò xo tương đương khi 2 lò xo mắc song song là:
-
Một con lắc lò xo nhẹ và vật nhỏ dao động điều hòa theo phương ngang với tần số góc 10 rad/s. Biết rằng khi động năng và thế năng bằng nhau thì vận tốc có độ lớn là 0,6m/s. Biên độ dao động của con lắc là:
-
Một con lắc lò xo thẳng đứng, đầu dưới treo vật m dao động theo phương thẳng đứng trùng với trục của lò xo với phương trình x = 2cosωt (cm) (gốc tọa độ tại vị trí cân bằng. Biết tại vị trí cân bằng lò xo dãn một đoạn lớn hơn 2 cm. Tỉ số giữa lực cực đại và cực tiểu tác dụng vào điểm treo trong quá trình dao động là 3. Lấy gia tốc trọng trường g = π2 m/s2. Tần số góc dao động của vật là:
-
Một con lắc lò xo đang dao động tắt dần. Độ giảm cơ năng sau một thời gian là 14%. Tính độ giảm biên độ trong thời gian đó.
-
Khi gắn quả nặng m1 vào một lò xo, nó dao động với chu kỳ T1 = 1,2s. Khi gắn quả nặng m2 vào một lò xo, nó dao động với chu kỳ T2 = 1,6s. Khi gắn đồng thời m1 và m2 vào lò xo đó thì chu kỳ dao động của chúng là
-
Một vật có khói lượng m khi treo vào lò xo có độ cứng K1 thì dao động với chu kỳ \({T_1} = 0,64{\rm{s}}.\) Nếu mắc vật m trên vào lò xo có độ cứng K2 thì nó dao động với chu kỳ là \({T_2} = 0,36s\) . Mắc hệ nối tiếp 2 lò xo thì chu kỳ dao động của hệ là bao nhiêu?
-
Cho hệ vật gồm lò xo nhẹ có độ cứng k = 20 N/m, vật M có khối lượng 30 g được nối với vật N có khối lượng 150 g bằng một sợi dây không dãn vắt qua ròng rọc như hình bên. Bỏ qua mọi ma sát, bỏ qua khối lượng dây và ròng rọc. Ban đầu giữ M tại vị trí để lò xo không biến dạng, N ở xa mặt đất. Thả nhẹ M để cả hai vật cùng chuyển động, sau 0,2 s thì dây bị đứt. Sau khi dây đứt, M dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Lấy g = 10m/s2, \(\pi ^2 \approx 10\) .Giá trị của A bằng
