ADMICRO
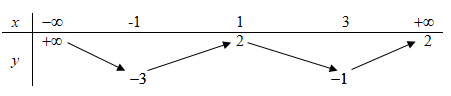
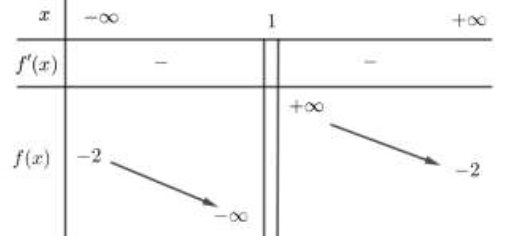
Đồ thị hàm số có đường tiệm cận đứng là:
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiVì và nên
Tương tự nên là tiệm cận đứng,
ZUNIA9
AANETWORK