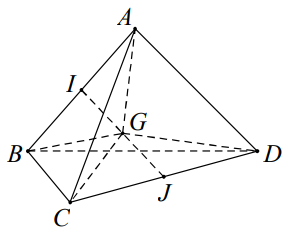
Cho tứ diện ABCD . Người ta định nghĩa “G là trọng tâm tứ diện ABCD khi \(\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}+\overrightarrow{G D}=\overrightarrow{0}\)”. Khẳng định nào sau đây sai? 

Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tâm O . Đặt \(\overrightarrow{A B}=\vec{a} ; \overrightarrow{B C}=\vec{b}\). M là điểm xác định bởi \(\overrightarrow{O M}=\frac{1}{2}(\vec{a}-\vec{b})\) . Khẳng định nào sau đây đúng? 

Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\), M là trung điểm của BB' . Đặt \(\overrightarrow{C A}=\vec{a}, \overrightarrow{C B}=\vec{b}, \overrightarrow{A A^{\prime}}=\vec{c}\). Khẳng định nào sau đây đúng? 

Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{M N}=k(\overrightarrow{A D}+\overrightarrow{B C})\)

Cho ba vecto \(\vec a,\;\vec b,\;\vec c\). Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.

Cho tứ diện ABCD . Gọi M, N  lần lượt là trung điểm của AB, CD và G là trung điểm của MN . Trong các khẳng định sau, khẳng định nào sai? 

Cho hình chóp S.ABCD, với O là giao điểm của AC và BD. Mệnh đề nào sau đây là đúng?

Tìm véctơ \(\vec u\) biết rằng véctơ \(\vec u\) vuông góc với véctơ \(\vec a\) = (1;−2;1) và thỏa mãn \(\vec u.\vec b = - 1;{\mkern 1mu} {\mkern 1mu} \vec u.\vec c = - 5\) với \(\vec b = \left( {4; - 5;2} \right),{\mkern 1mu} {\mkern 1mu} \vec c = \left( {8;4; - 5} \right).\)

Cho hình hộp \(A B C D \cdot A_{1} B_{1} C_{1} D_{1}\) . Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{A B}+\overrightarrow{B_{1} C_{1}}+\overrightarrow {D D_{1}}=k \overrightarrow {A C_{1}}\)

Cho hình lập phương ABCD.EFGH  có cạnh bằng a . Ta có \( \overrightarrow{A B} \cdot \overrightarrow{E G}\) bằng? 

Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có cạnh bằng a . Hãy tìm mệnh đề sai trong những
mệnh đề sau đây: 

Cho ba vectơ \(\vec{a}, \vec{b}, \vec{c}\) không đồng phẳng. Xét các vectơ \(\vec{x}=2 \vec{a}+\vec{b} ; \vec{y}=\vec{a}-\vec{b}-\vec{c} ; \vec{z}=-3 \vec{b}-2 \vec{c}\).Chọn khẳng định đúng? 

Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.

\(\overrightarrow {AB} \; + \;\overrightarrow {AC} \; + \;\overrightarrow {AD} \) bằng:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.

Từ A hạ AH ⊥ SM. Khi đó góc giữa hai vecto \(\overrightarrow {SA} \) và \(\overrightarrow {AH} \) bằng:

Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có tâm O . Gọi I là tâm hình bình hành ABCD . Đặt \(\overrightarrow {A C^{\prime}}=\vec{u},\overrightarrow{C A^{\prime}}=\vec{v}, \overrightarrow{B D^{\prime}}=\vec{x}, \overline{D B^{\prime}}=\bar{y}\) . Trong các đẳng thức sau, đẳng thức nào đúng? 

Trong không gian với hệ tọa độ Oxyz,  cho tứ diện ABCD có A(2;−1;1),  B(3;0;−1), C(2;−1;3) và D thuộc trục Oy Tính tổng tung độ của các điểm D, biết thể tích tứ diện bằng 5 .

Cho vecto \(\vec n\; \ne \;\vec 0\) và hai vecto \(\vec a\) và \(\vec b\) không cùng phương. Nếu vecto \(\vec n\) vuông góc với cả hai vecto \(\vec a\) và \(\vec b\) thì \(\vec n\), \(\vec a\) và \(\vec b\):

Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Đặt \(\vec{x}=\overrightarrow{A B} ; \vec{y}=\overrightarrow{A C} ; \vec{z}=\overrightarrow{A D}\) . Khẳng định nào sau đây đúng

Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.

Bộ ba vecto đồng phẳng là:

Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc phẳng đỉnh B đều bằng 60^o.

Đường thẳng B’C vuông góc với đường thẳng:

Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.

Bộ ba vecto không đồng phẳng là: