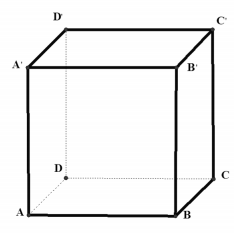
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) có cạnh bằng a . Hãy tìm mệnh đề sai trong những
mệnh đề sau đây:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
\(\begin{array}{l} \text { Ta có : } 2 \overrightarrow{A B}+\overrightarrow{B^{\prime} C^{\prime}}+\overrightarrow{C D}+\overrightarrow{D^{\prime} A^{\prime}}=\overrightarrow{0} \\ \Leftrightarrow \overrightarrow{A B}+(\overrightarrow{A B}+\overrightarrow{C D})+\left(\overline{B^{\prime} C^{\prime}}+\overrightarrow{D^{\prime} A^{\prime}}\right)=\overrightarrow{0} \\ \Leftrightarrow \overrightarrow{A B}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0} \Leftrightarrow \overrightarrow{A B}=\overrightarrow{0} \text { (vô lí) } \end{array}\)
Câu hỏi liên quan
-
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = (1;m;2);\overrightarrow b = (m + 1;2;1);\overrightarrow c = (0;m - 2;2)\). Giá trị m bằng bao nhiêu để ba vectơ\(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Gọi I và K lần lượt là tâm của hình bình hành \(A B B^{\prime} A^{\prime}\) và \(B C C^{\prime} B\) . Khẳng định nào sau đây sai?
-
Cho tứ diện ABCD . Gọi M và P lần lượt là trung điểm của AB và CD . Đặt \(\overrightarrow{A B}=\vec{b},\overrightarrow{A C}=\vec{c}, \overrightarrow{A D}=\vec{d}\). Khẳng định nào sau đây đúng?
-
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) với tâm O . Hãy chỉ ra đẳng thức sai trong các đẳng thức sau đây:
-
Cho tứ diện ABCD . Gọi M và N lần lượt là trung điểm của AB và CD . Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{M N}=k(\overrightarrow{A C}+\overrightarrow{B D})\)
-
Cho hình hộp \(A B C D \cdot A_{1} B_{1} C_{1} D_{1}\) . Trong các khẳng định sau, khẳng định nào sai?
-
Cho hình chóp S.ABCD, với O là giao điểm của AC và BD. Mệnh đề nào sau đây là đúng?
-
Cho ba vectơ\(\vec{a}, \vec{b}, \vec{c}\) không đồng phẳng. Trong các khẳng định sau, khẳng định nào sai?
-
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A′B′C′D′ biết A(1;0;1), B(2;1;2), D(1;−1;1) và C′(4;5;−5). Khi đó, thể tích của hình hộp đó là:
-
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;4;2), B(−1;2;4). Tìm tọa độ điểm M thuộc trục Oz sao cho :MA2+MB2 = 32.
-
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Vecto \(\overrightarrow {B'C} \) bằng:
-
Tìm véctơ \(\vec u\) biết rằng véctơ \(\vec u\) vuông góc với véctơ \(\vec a\) = (1;−2;1) và thỏa mãn \(\vec u.\vec b = - 1;{\mkern 1mu} {\mkern 1mu} \vec u.\vec c = - 5\) với \(\vec b = \left( {4; - 5;2} \right),{\mkern 1mu} {\mkern 1mu} \vec c = \left( {8;4; - 5} \right).\)
-
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt \(\vec{x}=\overrightarrow{A B} ; \vec{y}=\overrightarrow{A C} ; \vec{z}=\overrightarrow{A D}\) . Khẳng
định nào sau đây đúng? -
Điều kiện cần và đủ để ba vecto \(\vec a,\;\vec b,\;\vec c\) không đồng phẳng là:
-
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA'} \; = \;\vec a,\;\overrightarrow {AB} \; = \;\vec b,\;\overrightarrow {AC} \; = \;\vec c\)
Vecto \(\overrightarrow {AG} \) bằng:
-
Cho ba vectơ \(\vec{a}, \vec{b}, \vec{c}\) không đồng phẳng. Xét các vectơ \(\vec{x}=2 \vec{a}+\vec{b} ; \vec{y}=\vec{a}-\vec{b}-\vec{c} ; \vec{z}=-3 \vec{b}-2 \vec{c}\).Chọn khẳng định đúng?
-
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Tìm giá trị của k thích hợp điền vào đẳng thức vectơ \(\overrightarrow{A C}+\overrightarrow{B A^{\prime}}+k\left(\overrightarrow{D B}+\overrightarrow{C^{\prime} D}\right)=\overrightarrow{0}\)
-
Cho hình hộp \(A B C D \cdot A_{1} B_{1} C_{1} D_{1}\) . Chọn đẳng thức sai?
-
Cho tứ diện ABCD có AB = AC = AD; góc BAC = góc BAD = 60oBAD = 60o. Hãy chứng mình AB ⊥ CD.
Một bạn chứng mình qua các bước sau:
Bước 1. \(\overrightarrow {CD} \; = \;\overrightarrow {AC} \; - \;\overrightarrow {AD} \)
Bước 2. \(\overrightarrow {AB} .\overrightarrow {CD} \; = \;\overrightarrow {AB} .\left( {\overrightarrow {AC} \; - \;\overrightarrow {AD} } \right)\)
Bước 3. \(\overrightarrow {AB} .\overrightarrow {AC} \; - \;\overrightarrow {AB} .\overrightarrow {AD} \; = \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} \;} \right|.\cos {60^o}\; - \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} } \right|.\cos {60^o}\; = \;0\)
Bước 4. Suy ra AB ⊥ CD
Theo em. Lời giải trên sai từ:
-
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto không đồng phẳng là:
