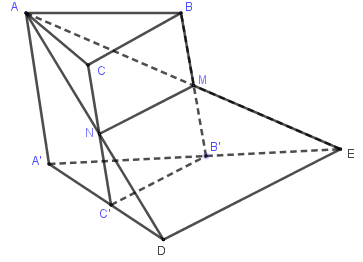
Cho hình lăng trụ (ABC.A'B'C' ). Gọi (M,N ) lần lượt là trung điểm của (BB',CC' ) và đường thẳng (\(\Delta\)) là giao tuyến của hai mặt phẳng (AMN) và (A'B'C'). Khẳng định nào sau đây đúng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi
\(\begin{array}{l} D = AN \cap A'C' \Rightarrow D \in \left( {AMN} \right) \cap \left( {A'B'C'} \right)\\ E = AM \cap A'B' \Rightarrow E \in \left( {AMN} \right) \cap \left( {A'B'C'} \right) \end{array}\)
Khi đó \( DE = \left( {AMN} \right) \cap \left( {A'B'C'} \right) = {\rm{\Delta }}\)
Lại có:
\(\left\{ \begin{array}{l} (AMN) \cap (MNC\prime B\prime ) = MN\\ (A\prime B\prime C\prime ) \cap (MNC\prime B\prime ) = B\prime C\prime \\ (AMN) \cap (A\prime B\prime C\prime ) = DE\\ MN//B\prime C\prime \end{array} \right.\)⇒ MN//B′C′//DE (định lý ba giao tuyến)
Do đó DE//B′C′//BC