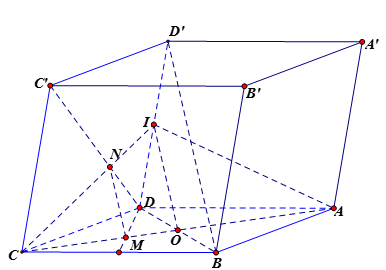
Cho hình hộp (ABCD.A'B'C'D' ). Gọi (M ) là điểm trên cạnh (AC ) sao cho (AC = 3MC ). Lấy (N ) trên cạnh (C'D ) sao cho (C'N = xC'D ). Với giá trị nào của (x ) thì (MN //BD' ).
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Ta có: MM là điểm trên cạnh AC sao cho AC=3MC. Nên M là trọng tâm của tam giác BCD.
Gọi O và I lần lượt là trung điểm của AC và DD′. Khi đó ta có: BD′//(IAC)
Trong (CDD′C′), gọi N′=CI∩C′D. Suy ra N′ là trọng tâm tam giác CDD′
Do đó: \( \frac{{CM}}{{CO}} = \frac{2}{3} = \frac{{CN'}}{{CI}} \Rightarrow MN'\://\:OI\) mà OI//BD′ nên MN′//BD′
Vậy N′≡N và \( x = \frac{2}{3}\)
Câu hỏi liên quan
-
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. kết luận nào sau đây là đúng?
-
Ký hiệu nào sau đây sai
-
Trong các mệnh đề sau, những mệnh đề nào đúng?
(1) Hai đường thẳng chéo nhau thì không có điểm chung.
(2) Hai đường thẳng không có điểm chung thì chéo nhau.
(3) Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng.
(4) Hai đường thẳng không song song thì chéo nhau.
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Lấy điểm I trên đoạn SO sao cho \(\dfrac{SI}{SO}=\dfrac23\), BI cắt SD tại M và DI cắt SB tại N. MNBD là hình gì ?
-
Trong không gian có bao nhiêu vị trí tương đối giữa đường thẳng và mặt phẳng?
-
Cho tứ diện ABCD, M là điểm thuộc BC sao cho MC = 2MB. N, P lần lượt là trung điểm của BD và AD. Điểm Q là giao điểm của AC với (MNP). Tính \(\frac{{QA}}{{QC}} \)
-
Cho tứ diện ABCD . M là điểm nằm trong tam giác ABC,mpα qua M và song song với AB và CD. Thiết diện của ABCD cắt bởi mpα là:
-
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M là điểm trên cạnh BC sao cho MB=2MC. Khi đó đường thẳng MG song song với mặt phẳng nào dưới đây?
-
Cho hai đường thẳng phân biệt a, b. Trong các điều kiện sau, điều kiện nào đủ để kết luận được hai đường thẳng a và b song song với nhau
-
Cho hình tứ diện ABCD và các điểm M, N, M’, N’ như hình vẽ ( M khác M’, N khác N’). Hai đường thẳng MN và M’N’
-
Cho hai đường thẳng a và b cùng song song với mpP. Khẳng định nào sau đây không sai?
-
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (AMN) và mp (BCD) là:
-
Cho tứ diện ABCD, M, N lần lượt là trọng tâm của tam giác ABC, ABD. Những khẳng định nào sau đây là đúng?
(1) MN //(BCD)
(2) MN //(ACD)
(3) MN // (ABD)
-
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là AB. M là trung điểm CD. Mặt phẳng α qua M song song với BC và SA. α cắt AB,SB lần lượt tại N và P. Nói gì về thiết diện của mặt phẳng α với khối chóp S.ABCD ?
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Khẳng định nào sau đây SAI?
-
Diện tích hình phẳng được giới hạn như hình vẽ được tính bởi công thức nào sau đây?
.png)
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm tam giác BCD. Khi ấy giao tuyến của MG và mặt phẳng (ABC) là
-
Với giả thiết: hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Ta có:
-
Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
