ADMICRO
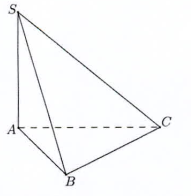
Cho hình chóp SABC, ΔABC vuông cân tại A, SA⊥(ABC), BC = a,((SBC),(ABC))=45o. Trên tia đối của tia SASA lấy điểm RR sao cho RS = 2SA. Tính VRABC
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo sai.png)
Gọi M là trung điểm của BC. Dễ thấy
Tam giác ABC vuông cân tại A suy ra .
Tam giác SAM vuông tại
Vậy
Mà
ZUNIA9
AANETWORK



.png)











