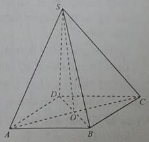
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M,N lần lượt là trung điểm của BC và SD. Gọi \(\alpha \) là góc giữa đường thẳng MN và đáy. Khẳng định nào sau đây đúng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi H là trung điểm của \(AB \Rightarrow SH \bot \left( {ABCD} \right)\).
Gọi P là trung điểm của HD, khi đó NP là đường trung bình của tam giác SHD, suy ra
\(NP = \frac{1}{2}SH = \frac{1}{2}.\frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{4}a\) và \(NP \bot \left( {ABCD} \right)\).
Hình chiếu vuông góc của MN lên mặt phẳng \(\left( {ABCD} \right)\) là MP, cho nên:
\(\left( {MN,\left( {ABCD} \right)} \right) = \left( {MN,MP} \right) = \widehat {PMN}\).
MP là đương trung bình của hình thang BCDH nên ta có: \(MP = \frac{{BH + CD}}{2} = \frac{{a + \frac{a}{2}}}{2} = \frac{{3a}}{4}\).
Trong tam giác vuông MNP ta có:
\(\tan \alpha = \tan \widehat {PMN} = \frac{{NP}}{{MP}} = \frac{{\sqrt 3 }}{3} \Rightarrow \alpha = 30^\circ \)
Câu hỏi liên quan
-
Khẳng định nào sau đây đúng?
-
Cho tứ diện đều S.ABC có tất cả các cạnh bằng nhau. Gọi \(M,\,N\) lần lượt là trung điểm của SA và BC. Tính cos góc giữa đường thẳng MN và mặt phẳng \(\left( {SBC} \right)\)
-
Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu H của S trên ( ABC) là:
-
Cho tứ diện S.ABC có đáy ABC là tam giác vuông cân tại B, các tam giác SAB và SBC lần lượt là các tam giác vuông tại A và C. Góc giữa đường thẳng SA và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^\circ \). Gọi H là hình chiếu vuông góc của S lên \(\left( {ABC} \right)\) và M là trung điểm của đoạn SA. Tính góc giữa đường thẳng HM mặt phẳng \(\left( {SBC} \right)\).
-
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:
-
Tìm mệnh đề đúng trong các mệnh đề sau:
-
Cho hình lập phương ABCD.A’B’C’D’. Tính \({\mathop{\rm Cos}\nolimits} in\) giữa đường thẳng A’C và mặt phẳng \(\left( {ABB’A’} \right)\)
-
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Góc giữa đường thẳng SA và mặt phẳng \(\left( {ABCD} \right)\) bằng:
-
Cho hình lập phương ABCD. A’B’C’D’. AA’ vuông góc với mặt phẳng.
-
Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD
Đường thẳng AC vuông góc với mặt phẳng
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Gọi \(\alpha\) là góc giữa AC ' và mp (A'BCD') . Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hình lập phương ABCD.A’B’C’D’. Xác định góc giữa đường thẳng A’C và mặt phẳng \(\left( {ABCD} \right)\)
-
Cho tứ diện SABC thoả mãn \(S A=S B=S C\) . Gọi H là hình chiếu của S lên mp ( ABC) . Đối với \(\Delta A B C\)ta có điểm H là:
-
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính góc giữa đường thẳng SA và mặt phẳng \(\left( {SBC} \right)\)
-
Cho hình chóp \(S \cdot A B C \text { có } S A=S B=S C\) và tam giác ABC vuông tại B . Vẽ \(S H \perp(A B C), H \in(A B C)\). Khẳng định nào sau đây đúng?
-
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:
.png)
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, Gọi H là trung điểm của AB và \(S H \perp(A B C D)\). Gọi K là trung điểm của cạnh AD . Khẳng định nào sau đây là sai?
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, biết \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 5 \). Gọi M là trung điểm của SB. Tính góc giữa đường thẳng CM và \(\left( {ABCD} \right)\)
-
Cho hình lập phương ABCD.A’B’C’D’: Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
