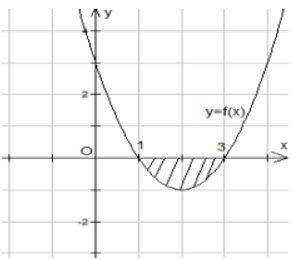
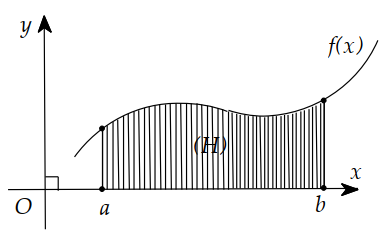
Cho hàm số \(y = {x^3} - 3x + 2\) (C). Gọi d là phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ \({x_0} = 2\). Tính diện tích hình phẳng giới hạn bởi đồ thị (C), tiếp tuyến d và đường thẳng x = 1.

Hình phẳng giới hạn bởi đồ thị hàm số \(y=1-\frac{1}{x^{2}}\), trục Ox và hai đường thẳng \(x=\frac{1}{2}, x=2\) có diện tích là

Cho hình phẳng \(\displaystyle  H\) giới hạn bởi các đường \(\displaystyle  y = f\left( x \right)\), \(\displaystyle  y = 0\), \(\displaystyle  x = b\) và \(\displaystyle  x = a\) (trong đó hàm số \(\displaystyle  f\left( x \right)\) liên tục trên đoạn \(\displaystyle  \left[ {b;a} \right]\)). Thể tích khối tròn xoay tạo nên bởi phép quay hình \(\displaystyle  H\) quanh trục \(\displaystyle  Ox\) được cho bởi công thức:

Diện tích của hình phẳng giới hạn bởi các đường \(y = x^2+ 1 , y = 0, x = - 1, x = 2 \) bằng:

Trên mặt phẳng Oxy, cho hình phẳng ( ) H giới hạn bởi các đường \(\begin{aligned} &(P): y=x^{2},\left(P^{\prime}\right): y=4 x^{2} \text { và } \text { (d): } y=4 \end{aligned}\) . Thể tích của khối tròn xoay khi quay (H ) quanh trục
Ox bằng

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f( x ),y = g( x ) \) và hai đường thẳng x = a,x = b (a < b) là:

Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{{x \over 2}}},y = 0,x = 0\) và \(x = 1\).
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f( x ) = x^2 - 1\), trục hoành và hai đường thẳng x =  - 1; x =  - 3 là:

Tính diện tích hình phẳng giới hạn bởi các đường: \(y = {x^2} - 3x + 2\) và \(y=x-1\).

Thể tích của một vật thể tròn xoay được tạo bởi một hình phẳng giới hạn bởi các đường: \(y = \cos x{\rm{ }};x = 0;x = \pi \) và quay quanh trục Ox.

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sin x, trục hoành, trục tung và đường  thẳng \(x = 2\pi \)

Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y=-2x-4\), trục hoành, trục tung và đường thẳng \(x=-2\).

Thể tích của khối tròn xoay tạo nên do quay quanh trục \(\displaystyle  Ox\) hình phẳng giới hạn bởi các đường \(\displaystyle  y = {\left( {1 - x} \right)^2},y = 0\), \(\displaystyle  x = 0\) và \(\displaystyle  x = 2\) bằng

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi \)

Quay hình phẳng (H) như hình được tô đậm trong hình vẽ bên quanh trục Ox ta được khối tròn xoay
có thể tích là

Tại một noiw không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật \(v(t)=10 t-t^{2}\), trong đó t ( phút) là thời gian tính từ lúc bắt đầu chuyển động, v(t) được  tính theo đơn vị mét/phút (m/p). Nếu như vậy thì bắt đầu tiếp đất vận tốc v của khí cầu là?
 

Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle  y = {x^3} - 1\) và tiếp tuyến với \(\displaystyle  y = {x^3} - 1\) tại điểm \(\displaystyle  \left( { - 1; - 2} \right)\).

Một vật bắt đầu chuyển động \(v(t)=2 t^{3}-15 t^{2}+24 t+20(\mathrm{~m} / \mathrm{s})\) . Hỏi trong 5 giây đầu tiên, quãng đường vật đi được cho đến khi đạt vận tốc lớn nhất là bao nhiêu? 

Tính diện tích hình phẳng giới hạn bởi các đường sau: \(\displaystyle  y = x - 1 + \frac{{\ln x}}{x},y = x - 1\) và \(\displaystyle  x = e\)

Hình phẳng giới hạn bởi đường elip \((E): x^{2}+16 y^{2}=16\) có diện tích bằng

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3} - 3{x^2} + 2x\), trục hoành, trục tung và đường thẳng \(x = 3\)