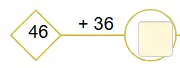
Trả lời:
Đáp án đúng: 6
100 - 94 = 6
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I - Toán 2 - Kết Nối Tri Thức Với Cuộc Sống - Bộ Đề 01 được biên soạn bám sát chương trình Toán lớp 2, giúp học sinh ôn tập và củng cố các kiến thức trọng tâm đã học trong học kì I như cộng, trừ trong phạm vi 1000, phép nhân – chia đơn giản, đo lường độ dài, khối lượng và nhận biết hình học cơ bản. Bộ đề gồm các câu hỏi trắc nghiệm và tự luận, được phân theo nhiều mức độ, giúp học sinh rèn luyện kỹ năng tính toán, tư duy logic và khả năng vận dụng kiến thức vào thực tế. Đây là tài liệu hữu ích cho học sinh ôn luyện và giáo viên, phụ huynh trong việc hỗ trợ học tập.
23/10/2025
0 lượt thi
0 / 18
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026