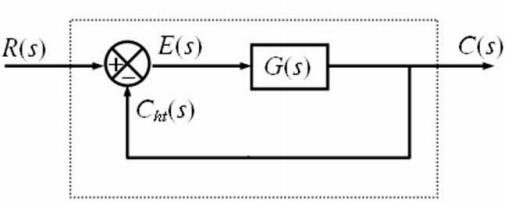
Biểu thức sai số xác lập cho hệ thống sau:
.png)
A.
\({e_{xl}} = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)H(s)}}\)
B.
\({e_{xl}} = \mathop {\lim }\limits_{s \to \infty } \frac{{sR(s)}}{{1 + G(s)H(s)}}\)
C.
\({e_{xl}} = \mathop {\lim }\limits_{s \to \infty } \frac{{R(s)}}{{1 + G(s)H(s)}}\)
D.
\({e_{xl}} = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + H(s)}}\)
Trả lời:
Đáp án đúng: A
Sai số xác lập (steady-state error) được tính bằng công thức:
\({e_{xl}} = \mathop {\lim }\limits_{s \to 0} sE(s)\), trong đó E(s) là sai lệch giữa tín hiệu vào R(s) và tín hiệu ra Y(s). Theo sơ đồ khối đã cho, ta có:
\(E(s) = R(s) - Y(s) = R(s) - G(s)E(s)H(s)\)
\(E(s) + G(s)E(s)H(s) = R(s)\)
\(E(s)[1 + G(s)H(s)] = R(s)\)
\(E(s) = \frac{R(s)}{{1 + G(s)H(s)}}\)
Do đó, sai số xác lập là:
\({e_{xl}} = \mathop {\lim }\limits_{s \to 0} sE(s) = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)H(s)}}\)
Vậy đáp án đúng là phương án 1.
Bộ 200+ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động có đáp án được tracnghiem.net chọn lọc và chia sẻ dưới đây, nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo!
50 câu hỏi 60 phút
Câu hỏi liên quan
Lời giải:
Đáp án đúng: D
Khâu động học cơ bản trong hệ thống điều khiển tự động bao gồm bốn loại chính: khâu khuếch đại (tăng ích), khâu tích phân, khâu vi phân và khâu trễ. Do đó, đáp án đúng là khâu nguyên hàm (tương đương với tích phân), khâu tích phân, khâu vi phân và khâu trễ.
Lời giải:
Đáp án đúng: A
Phương trình đặc tính của hệ thống hồi tiếp âm có dạng 1 + G(s)H(s) = 0, trong đó G(s) là hàm truyền của mạch hở và H(s) là hàm truyền của mạch hồi tiếp. Trong sơ đồ đã cho, ta thấy rõ đây là hệ hồi tiếp âm với hàm truyền mạch hở là G(s) và hàm truyền hồi tiếp là H(s). Do đó, phương trình đặc tính của hệ thống là 1 + G(s)H(s) = 0.
Lời giải:
Đáp án đúng: D
Câu hỏi này kiểm tra kiến thức về các phương pháp khảo sát tính ổn định của hệ thống liên tục.
- Tiêu chuẩn ổn định đại số Routh-Hurwitz: Đây là một phương pháp đại số để xác định tính ổn định của hệ thống dựa trên việc phân tích các hệ số của đa thức đặc trưng.
- Tiêu chuẩn ổn định tần số Mikhailov-Nyquist-Bode: Đây là các phương pháp tần số để xác định tính ổn định dựa trên đáp ứng tần số của hệ thống, sử dụng các đồ thị như Nyquist, Bode hoặc Mikhailov.
- Phương pháp chia miền ổn định: Phương pháp này thường dùng để xác định miền giá trị của các tham số để hệ thống ổn định.
- Phương pháp quỹ đạo nghiệm số: Phương pháp này vẽ quỹ đạo của các nghiệm của phương trình đặc trưng khi một tham số nào đó thay đổi. Từ đó, ta có thể đánh giá tính ổn định của hệ thống.
Dựa vào các phương pháp trên, ta thấy đáp án đúng là đáp án bao gồm cả ba phương pháp khảo sát chính: tiêu chuẩn ổn định đại số Routh-Hurwitz, tiêu chuẩn ổn định tần số Mikhailov-Nyquist-Bode, phương pháp chia miền ổn định và phương pháp quỹ đạo nghiệm số. Tuy nhiên, không có đáp án nào liệt kê đầy đủ và chính xác các phương pháp khảo sát tính ổn định của hệ thống liên tục. Đáp án số 4 liệt kê nhiều phương pháp nhất và bao hàm các phương pháp cơ bản.
- Tiêu chuẩn ổn định đại số Routh-Hurwitz: Đây là một phương pháp đại số để xác định tính ổn định của hệ thống dựa trên việc phân tích các hệ số của đa thức đặc trưng.
- Tiêu chuẩn ổn định tần số Mikhailov-Nyquist-Bode: Đây là các phương pháp tần số để xác định tính ổn định dựa trên đáp ứng tần số của hệ thống, sử dụng các đồ thị như Nyquist, Bode hoặc Mikhailov.
- Phương pháp chia miền ổn định: Phương pháp này thường dùng để xác định miền giá trị của các tham số để hệ thống ổn định.
- Phương pháp quỹ đạo nghiệm số: Phương pháp này vẽ quỹ đạo của các nghiệm của phương trình đặc trưng khi một tham số nào đó thay đổi. Từ đó, ta có thể đánh giá tính ổn định của hệ thống.
Dựa vào các phương pháp trên, ta thấy đáp án đúng là đáp án bao gồm cả ba phương pháp khảo sát chính: tiêu chuẩn ổn định đại số Routh-Hurwitz, tiêu chuẩn ổn định tần số Mikhailov-Nyquist-Bode, phương pháp chia miền ổn định và phương pháp quỹ đạo nghiệm số. Tuy nhiên, không có đáp án nào liệt kê đầy đủ và chính xác các phương pháp khảo sát tính ổn định của hệ thống liên tục. Đáp án số 4 liệt kê nhiều phương pháp nhất và bao hàm các phương pháp cơ bản.
Lời giải:
Đáp án đúng: B
Vị trí cân bằng ổn định là vị trí mà khi vật bị lệch khỏi vị trí đó một chút, nó sẽ có xu hướng tự trở về vị trí ban đầu. Trong hình, có hai vị trí như vậy: đáy của hai "lòng chảo".
Lời giải:
Đáp án đúng: B
Để lập phương trình trạng thái từ hàm truyền, ta thực hiện các bước sau:
1. Xác định bậc của mẫu số: Mẫu số của hàm truyền là \(s^3 + 6s^2 + 11s + 6\), có bậc là 3. Điều này cho biết hệ thống có 3 trạng thái.
2. Chọn dạng canonical (dạng điều khiển được): Trong dạng điều khiển được, ma trận A có cấu trúc đặc biệt, và các ma trận B và C có dạng đơn giản.
3. Xây dựng ma trận A: Với mẫu số \(s^3 + 6s^2 + 11s + 6\), ta có thể viết ma trận A như sau:
\(A = \left[ {\begin{array}{*{20}{c}}
0&1&0\\
0&0&1\\
{ - 6}&{ - 11}&{ - 6}
\end{array}} \right]\)
Các phần tử ở hàng cuối cùng của ma trận A là các hệ số của mẫu số, lấy dấu âm.
4. Xây dựng ma trận B: Với hàm truyền có tử số là 6, ma trận B sẽ là:
\(B = \left[ \begin{array}{l}
0\\
0\\
6
\end{array} \right]\)
5. Xây dựng ma trận C: Ma trận C sẽ là:
\(C = \left[ {1{\rm{ 0 0}}} \right]\)
Như vậy, phương trình trạng thái sẽ là:
\(A = \left[ {\begin{array}{*{20}{c}}
0&1&0\\
0&0&1\\
{ - 6}&{ - 11}&{ - 6}
\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}
0\\
0\\
6
\end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
Phương án 2 khớp với kết quả trên.
1. Xác định bậc của mẫu số: Mẫu số của hàm truyền là \(s^3 + 6s^2 + 11s + 6\), có bậc là 3. Điều này cho biết hệ thống có 3 trạng thái.
2. Chọn dạng canonical (dạng điều khiển được): Trong dạng điều khiển được, ma trận A có cấu trúc đặc biệt, và các ma trận B và C có dạng đơn giản.
3. Xây dựng ma trận A: Với mẫu số \(s^3 + 6s^2 + 11s + 6\), ta có thể viết ma trận A như sau:
\(A = \left[ {\begin{array}{*{20}{c}}
0&1&0\\
0&0&1\\
{ - 6}&{ - 11}&{ - 6}
\end{array}} \right]\)
Các phần tử ở hàng cuối cùng của ma trận A là các hệ số của mẫu số, lấy dấu âm.
4. Xây dựng ma trận B: Với hàm truyền có tử số là 6, ma trận B sẽ là:
\(B = \left[ \begin{array}{l}
0\\
0\\
6
\end{array} \right]\)
5. Xây dựng ma trận C: Ma trận C sẽ là:
\(C = \left[ {1{\rm{ 0 0}}} \right]\)
Như vậy, phương trình trạng thái sẽ là:
\(A = \left[ {\begin{array}{*{20}{c}}
0&1&0\\
0&0&1\\
{ - 6}&{ - 11}&{ - 6}
\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}
0\\
0\\
6
\end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
Phương án 2 khớp với kết quả trên.
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
