Cho biết có mấy vị trí cân bằng ổn định trong hình sau:

Trả lời:

Đáp án đúng: B

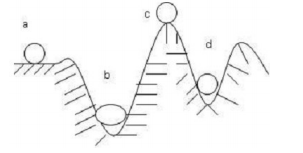
Vị trí cân bằng ổn định là vị trí mà khi vật bị lệch khỏi vị trí đó một chút, nó sẽ có xu hướng tự trở về vị trí ban đầu. Trong hình, có hai vị trí như vậy: đáy của hai "lòng chảo".

200+ câu trắc nghiệm Lý thuyết điều khiển tự động có đáp án - Phần 4

Bộ 200+ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động có đáp án được tracnghiem.net chọn lọc và chia sẻ dưới đây, nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo!

50 câu hỏi 60 phút

Bắt đầu thi

Câu hỏi liên quan

Câu 34:

Cho hàm truyền ,hãy lập phương trình trạng thái:

Lời giải:

Đáp án đúng: B

Để lập phương trình trạng thái từ hàm truyền, ta thực hiện các bước sau:

1. Xác định bậc của mẫu số: Mẫu số của hàm truyền là \(s^3 + 6s^2 + 11s + 6\), có bậc là 3. Điều này cho biết hệ thống có 3 trạng thái.

2. Chọn dạng canonical (dạng điều khiển được): Trong dạng điều khiển được, ma trận A có cấu trúc đặc biệt, và các ma trận B và C có dạng đơn giản.

3. Xây dựng ma trận A: Với mẫu số \(s^3 + 6s^2 + 11s + 6\), ta có thể viết ma trận A như sau:
\(A = \left[ {\begin{array}{*{20}{c}}
0&1&0\\
0&0&1\\
{ - 6}&{ - 11}&{ - 6}
\end{array}} \right]\)
Các phần tử ở hàng cuối cùng của ma trận A là các hệ số của mẫu số, lấy dấu âm.

4. Xây dựng ma trận B: Với hàm truyền có tử số là 6, ma trận B sẽ là:
\(B = \left[ \begin{array}{l}
0\\
0\\
6
\end{array} \right]\)

5. Xây dựng ma trận C: Ma trận C sẽ là:
\(C = \left[ {1{\rm{ 0 0}}} \right]\)

Như vậy, phương trình trạng thái sẽ là:

\(A = \left[ {\begin{array}{*{20}{c}}
0&1&0\\
0&0&1\\
{ - 6}&{ - 11}&{ - 6}
\end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l}
0\\
0\\
6
\end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)

Phương án 2 khớp với kết quả trên.

Câu 35:

Hệ thống rời rạc bậc n được mô tả bằng:

Lời giải:

Đáp án đúng: B

Hệ thống rời rạc bậc n được mô tả bằng phương trình sai phân bậc n. Phương trình sai phân là một phương trình toán học mà nó xác định một dãy một cách đệ quy, trong đó số hạng tiếp theo của dãy là một hàm của một số số hạng trước đó. Bậc của phương trình sai phân được xác định bởi số lượng các giá trị quá khứ được sử dụng để tính toán giá trị hiện tại.

Câu 36:

Cho phương trình \({s^2} + 25{s^2} + 250s + 10 = 0\). Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm có phần thực dương:

Lời giải:

Đáp án đúng: A

Phương trình đặc trưng của hệ thống là s⁴ + 25s² + 250s + 10 = 0. Để xét tính ổn định của hệ thống, ta sử dụng tiêu chuẩn Routh-Hurwitz. Lập bảng Routh:

s⁴ | 1 25 10
s³ | 0 250 0
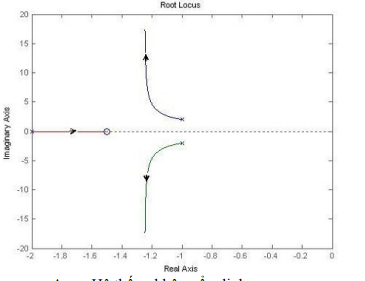
s² | Do phần tử đầu tiên của hàng s³ bằng 0, ta thay nó bằng ε (một số dương rất nhỏ) và tiếp tục tính toán. Tuy nhiên, để tránh các phép tính phức tạp với ε, ta có thể nhận thấy rằng phương trình đặc trưng có dạng s⁴ + 0s³ + 25s² + 250s + 10 = 0. Sự thay đổi dấu trong cột đầu tiên của bảng Routh cho biết số lượng nghiệm nằm bên phải mặt phẳng phức. Trong trường hợp này, hệ số của s³ bằng 0, trong khi các hệ số khác đều dương. Điều này cho thấy có ít nhất một nghiệm có phần thực dương, do đó hệ thống không ổn định. Để xác định số lượng nghiệm nằm bên phải mặt phẳng phức, cần phân tích kỹ hơn hoặc sử dụng các phương pháp khác (ví dụ: vẽ quỹ đạo nghiệm số). Tuy nhiên, do các đáp án chỉ đưa ra số lượng nghiệm bên phải mặt phẳng phức là 1, 2 hoặc 3, và hệ thống không ổn định, ta có thể suy luận đáp án phù hợp nhất. Dựa trên tiêu chuẩn Routh, ta thấy có sự thay đổi dấu, điều này chỉ ra hệ thống không ổn định. Số lượng nghiệm nằm bên phải mặt phẳng phức là 1 hoặc 2 hoặc 3. Đáp án phù hợp nhất là: Hệ thống không ổn định, có 1 nghiệm bên phải mặt phẳng phức, 2 nghiệm bên trái mặt phẳng phức.

Câu 37:

Các trạng thái cân bằng gồm:

Lời giải:

Đáp án đúng: C

Trong vật lý, có ba loại trạng thái cân bằng chính:

1. Cân bằng ổn định: Khi vật bị lệch khỏi vị trí cân bằng, nó có xu hướng tự trở về vị trí đó.
2. Cân bằng không ổn định: Khi vật bị lệch khỏi vị trí cân bằng, nó có xu hướng tiếp tục rời xa vị trí đó.
3. Cân bằng biên giới ổn định (hay còn gọi là cân bằng phiếm định/cân bằng bền vững): Khi vật bị lệch khỏi vị trí cân bằng, nó không có xu hướng trở về cũng không có xu hướng rời xa vị trí đó; nó sẽ ở trạng thái cân bằng mới.

Vì vậy, đáp án đầy đủ nhất phải bao gồm cả ba trạng thái này.

Câu 38:

Tần số cắt biên:

Lời giải:

Đáp án đúng: A

Tần số cắt biên (cutoff frequency) là tần số mà tại đó biên độ của đáp ứng tần số giảm xuống một mức nhất định so với biên độ ở tần số thấp. Thông thường, mức giảm này là -3dB, tương ứng với biên độ giảm xuống 1/√2 lần hoặc khoảng 70.7% so với biên độ tối đa. Trong lý thuyết điều khiển, tần số cắt biên thường được định nghĩa là tần số mà tại đó biên độ của đặc tính tần số vòng hở (open-loop frequency response) bằng 1 (hoặc 0dB). Điều này liên quan đến việc xác định tính ổn định và hiệu suất của hệ thống điều khiển.

Phương án 1 đúng vì nó mô tả chính xác định nghĩa của tần số cắt biên, tức là tần số mà biên độ của đặc tính tần số bằng 1 (0dB). Các phương án còn lại không đúng vì chúng mô tả các đặc điểm khác của hệ thống điều khiển, không phải định nghĩa của tần số cắt biên.

Câu 39:

Cho hệ có phương trình đặc trưng: \({s^4} + 2{s^3} + 2{s^2} + 8s + 1 = 0\)

Lời giải: