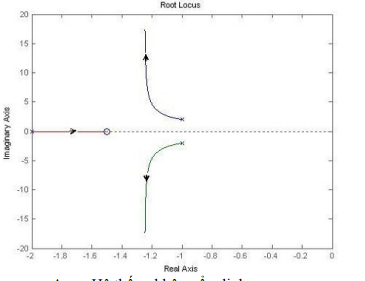
Cho hệ có phương trình đặc trưng: \({s^4} + 2{s^3} + 2{s^2} + 8s + 1 = 0\)
Trả lời:
Đáp án đúng: B
Để xét tính ổn định của hệ thống, ta sử dụng tiêu chuẩn Routh-Hurwitz. Từ phương trình đặc trưng \({s^4} + 2{s^3} + 2{s^2} + 8s + 1 = 0\), ta lập bảng Routh:
s^4 | 1 2 1
s^3 | 2 8 0
s^2 | -2 -1 0
s^1 | 6 0 0
s^0 | 1 0 0
Số lần đổi dấu của cột đầu tiên là 2 (từ 2 sang -2 và từ -2 sang 6). Do đó, có 2 nghiệm nằm bên phải mặt phẳng phức. Vậy hệ thống không ổn định và có 2 nghiệm có phần thực dương.
Bộ 200+ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động có đáp án được tracnghiem.net chọn lọc và chia sẻ dưới đây, nhằm giúp các bạn sinh viên có thêm tư liệu tham khảo!
50 câu hỏi 60 phút