Mạch điện xoay chiều gồm cuộn dây và tụ điện mắc nối tiếp, tụ điện có điện dung thay đổi được. Điện áp đặt vào 2 đầu mạch có giá trị hiệu dụng \(U=120V\), tần số không đổi. Khi dung kháng \({{Z}_{C}}<{{Z}_{Co}}\) thì luôn có 2 giá trị của \({{Z}_{C}}\) để công suất tiêu thụ của mạch bằng nhau. Khi \({{Z}_{C}}<{{Z}_{Co}}\) thì chỉ có 1 giá trị công suất của mạch tương ứng. Khi \({{Z}_{C}}={{Z}_{Co}}\) thì điện áp hiệu dụng giữa 2 đầu cuộn dây là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐáp án B
Công suất tiêu thụ trên mạch: \(P={{I}^{2}}R=\frac{{{U}^{2}}R}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\)
Khi \({{Z}_{C}}=0\) thì \){{P}_{0}}=\frac{{{U}^{2}}R}{{{R}^{2}}+Z_{L}^{2}}\) thì \({{P}_{\max }}=\frac{{{U}^{2}}}{R}\)
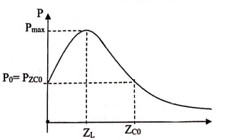
Đồ thị phụ thuộc của công suất P vào \({{Z}_{C}}\) như hình vẽ
+ Khi \({{Z}_{C}}<{{Z}_{C0}}\) thì luôn có 2 giá trị của \({{Z}_{C}}\) để công suất tiêu thụ của mạch bằng nhau.
+ Khi \({{Z}_{C}}>{{Z}_{C0}}\) thì chỉ có 1 giá trị công suất
+ Khi \({{Z}_{C}}={{Z}_{C0}}=2{{Z}_{L}}\) thì \({{P}_{ZC0}}={{P}_{0}}\)
Khi đó: \({{U}_{d}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C0}} \right)}^{2}}}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+Z_{L}^{2}}}=U=120\text{ }V\)
Câu hỏi liên quan
-
Khả năng đâm xuyên của bức xạ nào mạnh nhất trong các bức xạ sau?
-
Trên mặt nước hai nguồn đồng bộ A,B phát ra hai sóng kết hợp có bước sóng bằng 4 cm. Khi xảy ra giao thoa ổn định thì khoảng cách ngắn nhất giữa hai cực đại trên đoạn thẳng nối hai nguồn là
-
Trong các bức xạ phát ra từ nguồn là vật được nung nóng, bức xạ nào cần nhiệt độ của nguồn cao nhất ?
-
Đặt điện áp u = 200\(\sqrt 2 \)cos(100\(\pi \)t) (V) vào hai đầu đoạn mạch chỉ chứa điện trở thuần 50 \(\Omega \) thì cường độ dòng điện hiệu dụng qua mạch là
-
So với trong chân không thì bước sóng của ánh sáng đơn sắc trong môi trường có chiết suất n đối với ánh sáng đơn sắc này sẽ
-
Trong thí nghiệm Iâng về giao thoa ánh sáng, hai khe cách nhau \(a=1mm\) , hai khe cách màn quan sát một khoảng \(D=2m\) . Chiếu vào hai khe đồng thời hai bức xạ có bước sóng \({{\lambda }_{1}}=0,4\mu m\) và \({{\lambda }_{2}}=0,56\mu m\). Hỏi trên đoạn MN với \({{x}_{M}}=10mm\) và \({{x}_{N}}=30mm\) có bao nhiêu vạch đen cua 2 bức xạ trùng nhau?
-
Cho biết khối lượng hạt nhân \({}_{92}^{234}U\) là 233,9904 u. Biết khối lượng của hạt prôtôn và nơtrôn lần lượt là mp= 1,007276 u và mn= 1,008665 u. Độ hụt khối của hạt nhân \({}_{92}^{234}U\) bằng
-
Biết h là hằng số Plăng, c là tốc độ ánh sáng trong chân không Nếu trong một môi trường ta biết được bước sóng của lượng tử bằng λ và năng lượng là \(\varepsilon \), thì chiết suất tuyệt đối của môi trường đó bằng
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát đồng thời hai bức xạ đơn sắc, trong đó bức xạ màu đỏ có bước sóng \({{\lambda }_{d}}=720\,\,nm\) và bức xạ màu lục có bước sóng \({{\lambda }_{l}}\) (có giá trị trong khoảng từ 500 nm đến 575 nm). Trên màn quan sát, giữa hai vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có 8 vân sáng màu lục. Giá trị của \({{\lambda }_{l}}\) là :
-
Con lắc lò xo dao động điều hòa tự do trên mặt phẳng ngang dọc theo trục Ox với O là vị trí cân bằng, có phương trình dao động là x = 10cos(5πt) (cm). Biết khối lượng của vật nặng là 1 kg, lấy π² ≈ 10. Độ cứng của lò xo là
-
Bước sóng là:
-
Đồng vị nNa là chất phóng xạ β-, trong 10 giờ đầu người ta đếm được 1015 hạt β- bay ra. Sau 30 phút kể từ khi đo lần đầu người ta lại thấy trong 10 giờ đếm được 2,5.1014 hạt β- bay ra. Tính chu kỳ bán rã của đồng vị nói trên.
-
Để xác định một điểm trong không gian có từ trường hay không, ta đặt tại đó một
-
Một sóng truyền theo phương ngang AB. Tại một thời điểm nào đó, hình dạng sóng được biểu diễn như trên hình bên. Biết rằng điểm M đang đi lên vị trí cân bằng. Sau thời điểm này T/2 (T là chu kỳ dao động sóng) thì điểm N đang
-
Một con lắc đơn dao động điều hòa tại nơi có gia tốc g = π2 m/s2 với tần số góc π rad/s. Chiều dài của con lắc đơn là
-
Thí nghiệm giao thoa sóng ở mặt nước với hai nguồn kết hợp dao động cùng pha. Sóng do hai nguồn phát ra có bước sóng λ. Cực tiểu giao thoa cách hai nguồn những đoạn d1 và d2 thỏa mãn
-
Một vật dao động điều hòa, thương số giữa gia tốc và … có giá trị không đổi theo thời gian. Đại lượng còn thiếu trong dấu “…” là
-
Tại hai điểm A và B cách nhau 10 cm trong không khí, đặt hai điện tích \({q_1} = - 2,{7.10^{ - 6}}C\), \({q_2} = 6,{4.10^{ - 6}}C\). Xác định lực điện do hai điện tích này tác dụng lên \({q_3} = {4.10^{ - 6}}C\) đặt tại C. Biết AC = 6 cm, BC = 8 cm.
-
Công thoát êlectrôn (êlectron) ra khỏi một kim loại là A = 1,88 eV. Biết hằng số Plăng h = 6,625.10−34 J.s, vận tốc ánh sáng trong chân không c = 3.108m/s và 1 eV = 1,6.10−19 J. Giới hạn quang điện của kim loại đó là
-
Theo mẫu nguyên tử Bo, trong nguyên tử hiđrô, chuyển động của êlectron quanh hạt nhân là chuyển động tròn đều. Gọi v là tốc độ của electron trên quỹ đạo K. Khi nhảy lên quỹ đạo N, electron có tốc độ bằng
