Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB=1,AD=AA'=\sqrt{3}\). Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và \(BC\). Góc giữa 2 đường thẳng \(MN\) và \(AC\) bằng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai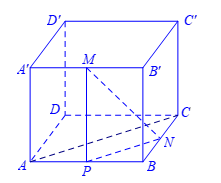
Xét tam giác \(ABC\) vuông tại \(B\Rightarrow AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2\).
Gọi \(P\) là trung điểm của \(AB\).
Khi đó \(NP\) là đường trung bình của tam giác \(ABC\).
\(\Rightarrow \left\{ \begin{align} & NP\text{//}AC \\ & NP=\frac{1}{2}AC=1 \\ \end{align} \right.\)
Do \(NP\text{//}AC\) nên \(\widehat{(MN,AC)}=\widehat{(MN,NP)}=\widehat{MNP}\).
Do \(M,P\) lần lượt là trung điểm của \({A}'{B}'\) và \(AB\Rightarrow MP=A{A}'=\sqrt{3}\).
Xét tam giác \(MNP\) vuông tại \(P\) có \(\tan \widehat{MNP}=\frac{MP}{NP}=\sqrt{3}\Rightarrow \widehat{MNP}={{60}^{0}}\).
Chọn B
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Minh Đức