Cho hàm số \(f(x)\) có đạo hàm \({f}'(x)=\frac{1}{2}{{x}^{2}}-2x+\frac{3}{2}\) và \(f(0)=0\). Có tất cả bao nhiêu số nguyên \(m\in \left( -2021\,;\,2022 \right)\) để hàm số \(g(x)=\left| {{f}^{2}}(x)+2f(x)+m \right|\) có đúng 3 điểm cực trị?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có: \(f(x)=\frac{1}{6}{{x}^{3}}-{{x}^{2}}+\frac{3}{2}x+C\).
Mà \(f(0)=0\)\(\Leftrightarrow C=0\).
Do đó, \(f(x)=\frac{1}{6}{{x}^{3}}-{{x}^{2}}+\frac{3}{2}x\).
Đặt \(h\left( x \right)={{f}^{2}}(x)+2f(x)+m\).
\({h}'\left( x \right)=2{f}'(x).f(x)+2{f}'(x)=2{f}'(x)\left( f(x)+1 \right)\).
\({h}'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & {f}'(x)=0 \\ & f(x)=-1 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=3\,\,\,\vee \,\,\,x=1 \\ & x=a\approx -0,4920 \\ \end{align} \right.\)
Bảng biến thiên của \(h\left( x \right)\)
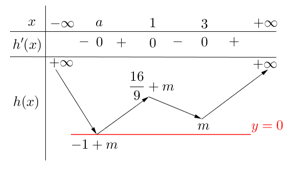
Từ bảng biến thiên, \(g(x)=\left| {{f}^{2}}(x)+2f(x)+m \right|=\left| h(x) \right|\) có đúng 3 điểm cực trị \(\Leftrightarrow 0\le -1+m\Leftrightarrow m\ge 1\). Mà
\(\left\{ \begin{align} & m\in \mathbb{Z} \\ & m\in \left( -2021\,;\,2022 \right) \\ \end{align} \right.\)
nên có \(2021\) giá trị \(m\) thỏa yêu cầu.
Chọn A
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Minh Đức
Câu hỏi liên quan
-
Cho khối lăng trụ có diện tích đáy bằng \(B\) và chiều cao bằng \(h\). Thể tích \(V\) của khối lăng trụ đã cho được tính theo công thức nào?
-
Trong không gian \(Oxyz\), cho 2 véctơ \(\vec{a}=\left( 2\,;\,3\,;\,2 \right)\) và \(\vec{b}=\left( 1\,;\,1\,;\,-1 \right)\). Véctơ \(\vec{a}-\vec{b}\) có toạ độ là?
-
Trong không gian \(Oxyz,\)gọi \(\left( P \right)\) là mp chứa đường thẳng \(d:\frac{x-2}{1}=\frac{y-1}{2}=\frac{z}{-1}\) và cắt trục \(Ox\,,\,Oy\) lần lượt tại \(A\) và \(B\) sao cho đường thẳng \(AB\) vuông góc với \(d\). Phương trình của mặt phẳng \(\left( P \right)\) là?
-
Cho khối nón đỉnh \(S\) có đáy là đường tròn tâm \(O\), bán kính \(R\). Trên đường tròn \(\left( O \right)\) lấy 2 điểm \(A,B\) sao cho tam giác \(OAB\) vuông. Biết diện tích tam giác \(SAB\) bằng \(\sqrt{2}{{R}^{2}}\). Thể tích khối nón đã cho bằng?
-
Tìm TXĐ của hàm số \(y={{\log }_{3}}\left( {{x}^{2}}-1 \right)\) là?
-
Trên tập hợp số phức, biết \({{z}_{0}}=3-2i\) là một nghiệm của phương trình \({{z}^{2}}+az+b=0\)(với \(a,\,\,b\in \mathbb{R}\)). Tính giá trị của \(a+b\) bằng?
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữa nhật, \(AB=2,\,AD=2\sqrt{3}\), tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc đáy, k/c giữa 2 đường thẳng \(AB\) và \(SC\)bằng \(3\). Tính thể tích của khối chóp \(S.ABCD\) bằng?
-
Cho CSC \(\left( {{u}_{n}} \right)\)biết \({{u}_{1}}=5,\,{{u}_{2}}=8\). Giá trị của \({{u}_{4}}\) bằng?
-
Hàm số nào sau đây có đồ thị là đường cong như hình?
-
Trong không gian \(Oxyz\), đường thẳng đi qua điểm \(M\left( 3;\,-1;\,2 \right)\) và có VTCP \(\overrightarrow{u}=\left( 4;\,5;\,-7 \right)\) có phương trình là?
-
Nghiệm của phương trình sau \({{3}^{x}}=7\) là?
-
Họ nguyên hàm của của hàm số sau đây \(f\left( x \right)={{x}^{2}}-3x\) là?
-
Môđun của số phức sau \(z=4-3i\) bằng?
-
GTLN của hàm số \(f\left( x \right)=2{{x}^{3}}-6x\) trên đoạn \(\left[ 0;2 \right]\) bằng?
-
Cho hàm số sau \(f(x)\)có đạo hàm \({f}'(x)=\frac{1}{\sqrt{1-3x}},\forall x\in \left( -\infty ;\frac{1}{3} \right)\) và \(f(-1)=\frac{2}{3}\). Biết \(F(x)\) là nguyên hàm của \(f(x)\) thỏa mãn \(F(-1)=0\). Giá trị của \(F\left( \frac{1}{4} \right)\) bằng?
-
Cho hàm số \(y=f(x)\) có đồ thị là đường cong như hình:
Đồ thị hàm số đã cho cắt trục hoành tại điểm nào?
-
Có tất cả bao nhiêu cặp số nguyên \(\left( x\,;\,y \right)\) thỏa mãn \({{2.3}^{x-1}}-{{\log }_{3}}\left( {{3}^{x-2}}+2y \right)=6y-x\,+1\) và \({{2022}^{-1}}\le y\le 2022\)?
-
Trong không gian \(Oxyz\), điểm nào thuộc đường thẳng \(d:\frac{x-1}{2}=\frac{y}{1}=\frac{z+1}{2}?\)
-
Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có tất cả các cạnh đều bằng \(2\) (tham khảo hình). K/c từ \(B\) đến mặt phẳng \(\left( AC{C}'{A}' \right)\) bằng?
-
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB=1,AD=AA'=\sqrt{3}\). Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và \(BC\). Góc giữa 2 đường thẳng \(MN\) và \(AC\) bằng?
