Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA=2a và vuông góc với (ABCD) . Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai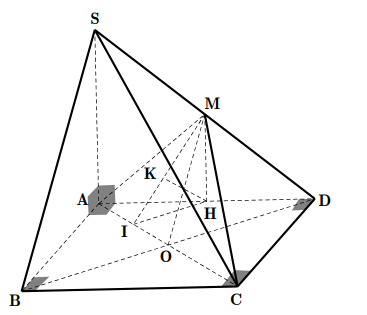
Gọi \(O=A C \cap B D\)
Vì ABCD là hình vuông cạnh a nên O là trung điểm của BD mà M là trung điểm của SD nên OM// SB / suy ra SB//(ACM).
Do đó \(d(S B, C M)=d(S B,(A C M))=d(B,(A C M))=d(D,(A C M))\)
Gọi H là trung điểm của AD nên \(M H / / S A \Rightarrow M H \perp(A B C D)\)
\(\Rightarrow d(S B, C M)=d(D,(A C M))=2 d(H,(A C M))\)
Kẻ \(H I \perp A C \Rightarrow(M H I) \perp(M A C)\) theo giao tuyến MI.
Kẻ \(H K \perp M I \Rightarrow H K \perp(A C M)\) hay \(d(H,(A C M))=H K\)
Ta có:
\(H I=\frac{1}{2} O D=\frac{1}{4} B D=\frac{1}{4} \sqrt{A B^{2}+A D^{2}}=\frac{a \sqrt{2}}{4}, M H=\frac{1}{2} S A=a\)
suy ra \(\frac{1}{H K^{2}}=\frac{1}{H M^{2}}+\frac{1}{H I^{2}} \Leftrightarrow \frac{1}{H K^{2}}=\frac{1}{a^{2}}+\frac{1}{\left(\frac{a \sqrt{2}}{4}\right)^{2}} \Leftrightarrow \frac{1}{H K^{2}}=\frac{9}{a^{2}} \Leftrightarrow H K=\frac{a}{3}\)
Vậy \(d(S B, C M)=2 d(H,(A C M))=2 H K=\frac{2 a}{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Bến Tre lần 1
Câu hỏi liên quan
-
Đồ thị hàm số \(y=f(x)\) với bảng biên thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm cận đứng bằng bao nhiêu?
-
Trong không gian toạ độ Oxyz, cho đường thẳng\(d:\left\{\begin{array}{l} x=2+3 t \\ y=5-4 t,(t \in \mathbb{R}) \\ z=-6+7 t \end{array}\right.\) và điểm A(1;2;3) . Đường thẳng đi qua A và song song với đường thẳng d có vectơ chỉ phương là:
-
Cho a và b là hai số thực dương thỏa mãn \(\log _{2}(a b)=\log _{4}\left(a b^{4}\right)\). Mệnh đề nào dưới đây đúng ?
-
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D'\) có các cạnh bằng 2a . Biết \(\widehat{B A D}=60^{\circ}, \widehat{A^{\prime} A B}=\widehat{A^{\prime} A D}=120^{\circ}\) Tính thể tích V của khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\)
-
Cho hàm sô y =f(x) thỏa mãn \(\left[f^{\prime}(x)\right]^{2}+f(x) \cdot f^{\prime \prime}(x)=x^{3}-2 x, \forall x \in R \text { và } f(0)=f^{\prime}(0)=2\) Tính giá trị của \(T=f^{2}(2)\)
-
Điểm M trong hình vẽ bên là điểm biểu diễn cho số phức z .
Ký hiệu\(\bar z\) là số phức liên hợp của z . Khi đó mệnh đề nào sau đây là đúng?
-
Cho hàm số\(y=f(x)=x^{4}-5 x^{2}+4\) có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng\(x=0, x=2\) (miền phẳng được gạch chéo trong hình vẽ). Mệnh đề nào sau đây sai?
-
Cho \(\int\limits_{1}^{2} f(x) \mathrm{d} x=-3 \text { và } \int\limits_{2}^{3} f(x) \mathrm{d} x=4\). Khi đó \(\int\limits_{1}^{3} f(x)dx\) bằng
-
Trong không gian Oxyz, cho mặt phẳng\((P): 5 x-2 y+z+6=0\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P) ?
-
Cho số phức z thỏa mãn \((3+2 i) z+(2-i)^{2}=4+i\). Hiệu phần thực và phần ảo của số phức z là
-
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng \(d: y=-x+m\) cắt đồ thị hàm số \(y=\frac{-2 x+1}{x+1}\) tại hai điểm phân biệt A B , sao cho\(A B \leq 2 \sqrt{2}\). Tổng giá trị các phần tử của S bằng
-
Cho hàm số y=f(x) biết hàm số f(x) có đạo hàm f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ . Đặt \(g(x)=f(x+1)\) . Kết luận nào sau đây đúng?
-
Cho bảng biến thiên của hàm số y =f(x) như hình vẽ. Phát biểu nào sau đây là sai?
-
Phương trình\(7^{2 x^{2}+5 x+4}=49\) có tổng các nghiệm bằng
-
Một hình trụ có bán kính đáy bằng chiều cao và bằng a . Một hình vuông ABCD có AB, CD là hai dây cung của hai đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng
-
Cho hàm số \(y=\left|x^{4}-2 x^{3}+x^{2}+a\right|\) . Có bao nhiêu số thực \(a \text { để } \min\limits _{[1 ; 2]} y+\max\limits _{[1 ; 2]} y=10 ?\)
-
Hàm số \(y=x^{3}+3 x^{2}+3 x-10\)có bao nhiêu điểm cực trị?
-
Rút gọn biểu thức \(P=x^{\frac{1}{2}} \sqrt[8]{x}\)
-
Cho cấp số nhân \((u_n)\) un với\(u_{1}=1, u_{3}=3\). Tính giá trị của \(u_7\) ?
-
Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
