Cho hàm số \(y = f(x)\). Đồ thị của hàm số \(y = f'(x)\) như hình bên. Đặt \(h(x) = 2f(x) - {x^2}\). Mệnh đề nào dưới đây đúng?
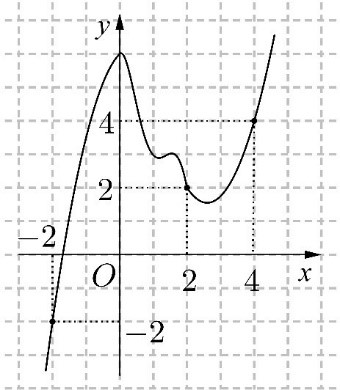
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi d là đường thẳng đi qua hai điểm (2;2) và (4;4), d có dạng: y=ax+b
Khi đó \(\left\{ \begin{array}{l}2a + b = 2\\4a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)
Suy ra phương trình của d là: y=x
Theo đề bài ta có:
\(h(x) = 2f(x) - {x^2} \Rightarrow h'(x) = 2f'(x) - 2x = 2\left[ {f'(x) - x} \right]\)
\(\begin{array}{l}\int\limits_2^4 {h'(x)dx} = \int\limits_2^4 {2[f'(x) - x{\rm{]}}dx} = - 2\int\limits_2^4 {\left[ {x - f'(x)} \right]dx} \\ \Leftrightarrow \left. {h(x)} \right|_2^4 = - 2{S_1} \Leftrightarrow h(4) - h(2) = - 2{S_1} < 0\\ \Rightarrow h(2) > h(4)\,\,\,(1)\end{array}\)
\(\begin{array}{l}\int\limits_{ - 2}^4 {h'(x)dx} = \int\limits_{ - 2}^4 {2\left[ {f'(x) - x} \right]dx} = 2\int\limits_{ - 2}^2 {\left[ {f'(x) - x} \right]dx} + 2\int\limits_2^4 {\left[ {f'(x) - x} \right]dx} \\ \Rightarrow \int\limits_{ - 2}^4 {h'(x)dx} = 2\int\limits_{ - 2}^2 {\left[ {f'(x) - x} \right]dx} - 2\int\limits_2^4 {\left[ {x - f'(x)} \right]dx} \\ \Leftrightarrow \left. {h(x)} \right|_{ - 2}^4 = 2({S_2} - {S_1}) \Leftrightarrow h(4) - h( - 2) = 2({S_2} - {S_1}) > 0\\ \Rightarrow h(4) > h( - 2)\end{array}\)
Từ (1) và (2) ta có: \(h(2) > h(4) > h( - 2).\)














