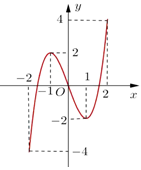
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây

Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có 6 nghiệm phân biệt

Tìm các số thực a và b thỏa mãn 2a + (b + i)i = 1 + 2i với i là đơn vị ảo.

Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ bên. Hàm số y = f(x) đạt cực đại tại điểm nào sau đây?

Cho hàm số y = f(x) có đạo hàm liên tục trên R thỏa mãn \(f'\left( x \right) - xf\left( x \right) = 0,f\left( x \right) > 0,\forall x \in R\) và f(0) = 1. Giá trị của f(1) bằng?

Cho biểu thức \(P=\sqrt[4]{{{x}^{5}}}\) với \(x>0\). Mệnh đề nào sau đây đúng?

Cho hàm số bậc bốn y = f(x) có đồ thị như hình dưới đây. Số nghiệm của phương trình \(3f\left( x \right) + 1 = 0\) là

Cho các số thực a, b, c thỏa mãn \({a^2} + {b^2} + {c^2} - 2a - 4b = 4\). Tính P = a + 2b + 3c khi biểu thức \(\left| {2a + b - 2c + 7} \right|\) đạt giá trị lớn nhất.

Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) là

Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 8 học sinh?

Cho a là số thực dương tùy ý, \(\ln \frac{e}{{{a^2}}}\) bằng

Cho hình chóp tam giác S.ABC có SA vuông góc với mặt phẳng \(\left( {ABC} \right),SA = \sqrt 3 .\) Tam giác ABC đều, cạnh a. Góc giữa SC và mặt phẳng (ABC) bằng:

Cho hình thang ABCD vuông tại A và D, AD = CD = a, AB = 2a. Quay hình thang ABCD quanh cạnh AB, thể tích khối tròn xoay thu được là :

Một lớp có 36 chiếc ghế đơn được xếp thành hình vuông 6 x 6. Giáo viên muốn xếp 36 học sinh của lớp, trong đó có em Kỷ và Hợi ngồi vào số ghế trên, mỗi học sinh ngồi một ghế. Xác suất để hai em Kỷ và Hợi ngồi cạnh nhau theo hàng dọc hoặc hàng ngang là

Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \(x(0 \le x \le 3)\) là một hình chữ nhật có hai kích thước là x và \(2\sqrt {9 - {x^2}} .\)

Họ nguyên hàm của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 3{\rm{x}} + 2}}\) là:

Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 8\). Công sai của cấp số cộng bằng

Một trong bốn hàm số cho trong các phương án A, B, c, D sau đây có đồ thị như hình vẽ

Hỏi hàm số đó là hàm số nào?

Trong không gian Oxyz, cho đường thẳng \({d_1}:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z - 3}}{1}\) và điểm \(A\left( {1;0; - 1} \right)\). Gọi \({d_2}\) là đường thẳng đi qua  A và có vecto chỉ phương \(\overrightarrow u  = \left( {a;1;2} \right)\). Giá trị của a sao cho đường thẳng \({d_1}\) cắt đường thẳng \({d_2}\) là

Nguyên hàm của hàm số \(y = \frac{1}{{1 - x}}\) là:

Cho hình lăng trụ \(ABC.{A}'{B}'{C}'\) và M, N là hai điểm lần lượt trên cạnh CA, CB sao cho MN song song với AB và \(\frac{CM}{CA}=k\). Mặt phẳng \(\left( MN{B}'{A}' \right)\) chia khối lăng trụ \(ABC.{A}'{B}'{C}'\) thành hai phần có thể tích \({{V}_{1}}\) (phần chứa điểm C) và \({{V}_{2}}\) sao cho \(\frac{{{V}_{1}}}{{{V}_{2}}}=2\). Khi đó giá trị của k là

Cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng \(\left( \alpha  \right):4x + 3y - 7z + 1 = 0\). Phương trình chính tắc của d là