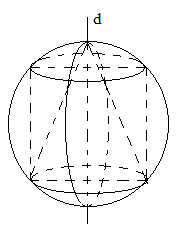
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Bán kính mặt cầu ngoại tiếp hình lập phương là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
\(\begin{array}{l}
AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \\
AC' = \sqrt {A{C^2} + CC{'^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3
\end{array}\)
Ta nhận thấy tâm I của mặt cầu ngoại tiếp hình lập phương chính là tâm của hình lập phương đó. Do đó I chính là trung điểm của AC’ và mặt cầu ngoại tiếp hình lập phương có bán kính là:
\(r = \frac{{AC'}}{2} = \frac{{a\sqrt 3 }}{2}\)
Câu hỏi liên quan
-
Một khối nón có thể tích bằng \(30\pi\), nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên 2 lần thì thể tích của khối nón mới bằng
-
Hình nón có bán kính đáy là 4a, chiều cao là 3a có diện tích xung quanh bằng:
-
Một hình trụ có đường kính của đáy bằng với chiều cao của nó. Nếu thể tích của khối trụ bằng \(2\pi\) thì chiều cao của hình trụ là
-
Trong số các khối trụ có thể tích bằng V, khối trụ có diện tích toàn phần bé nhất thì có bán kính đáy là
-
Cho hình nón có bán kính đáy \(r = \sqrt 3\), độ dài đường sinh l = 4. Tính diện tích xung quanh của hình nón đó?
-
Cho đường tròn tâm O bán kính r′. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA=h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau. Tính bán kính r của mặt cầu đi qua năm đỉnh của hình chóp.
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = 2a, AC = 2a. Hình chiếu của SS lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy (ABC) một góc 45o. Khoảng cách từ A đến mặt phẳng (SBC) là:
-
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, BC = \({a\sqrt 2 }\) và góc giữa A’B và mặt phẳng (ABC) là 60o. Bán kính của mặt cầu ngoại tiếp lăng trụ là:
-
Cho hình trụ có thiết diện qua trục là hình vuông có cạnh bằng (2a ). Thể tích của khối trụ giới hạn bởi hình trụ đã cho bằng:
-
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V1 là thể tích của thùng được theo cách 1 và V2 là tổng thể tích của hai thùng được theo cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)
-
Cho hình vẽ sau, chọn mệnh đề sai:
-
Mệnh đề nào dưới đây là sai?
-
Cho khối nón có thể tích bằng \(2\pi {a^3}\) và bán kính đáy bằng a. Độ dài đường sinh của khối nón đã cho bằng
-
Cho tam giác vuông cân ABC với AB = AC = a. Khi quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng đi qua B và song song với AC, ta được khối tròn có thể tích bằng
-
Cho hình trụ có bán kính đáy bằng a và diện tích toàn phần 6πa2a2. Diện tích của thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua các trục của hình trụ là:
-
Thể tích V của khối nón (N) có chiều cao bằng a và độ dài đường sinh bằng \(a\sqrt5\)
-
Thiết diện qua trục của hình trụ (T) là một hình vuông có cạnh bằng a. Diện tích
xung quanh của hình trụ (T) là -
Thể tích V của khối trụ có chiều cao bằng a và đường kính đáy bằng \(a\sqrt2\) là?
-
Cho hình nón có diện tích xung quanh là \({S_{xq}}\) và bán kính đáy là r. Công thức nào dưới đây dùng để tính đường sinh \(l\) của hình nón đã cho.
-
Cho hình trụ có bán kính đáy \(r=\sqrt 3\) và chiều cao h=4 . Diện tích xung quanh của hình trụ bằng.
