Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f’\left( x \right) = \frac{{\left( {x – 1} \right){{\left( {x – 2} \right)}^2}{{\left( {x – 3} \right)}^5}}}{{\sqrt[3]{{x – 4}}}}\). Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\\x = 3\end{array} \right.\).
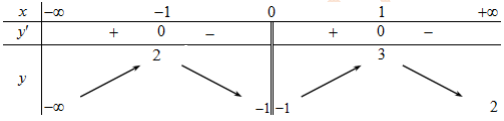
Bảng xét dấu của \(f’\left( x \right)\) như sau:
Do \(f’\left( x \right)\) đổi dấu khi x qua \(1,\;3,\;4\) nên hàm số \(y = f\left( x \right)\) có 3 điểm cực trị.
Câu hỏi liên quan
-
Điểm cực tiểu của đồ thị hàm số \(y = - {x^4} + 4{x^2} + 2\) là:
-
Tìm giá trị cực đại yCĐ của hàm số y = −x4+2x2−5
-
Biết đồ thị hàm số \(y = {x^3}\; - 3x + 1\) có hai điểm cực trị A,B . Khi đó phương trình đường thẳng AB là
-
Điểm cực tiểu của hàm số \(y=-x^{3}+3 x^{2}-3 x+2\) là
-
Cho hàm số y=x4−4x2−1. Gọi h1,h2 lần lượt là khoảng cách từ hai điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành. Khi đó tỷ số \(\frac{{{h_1}}}{{{h_2}}}\) bằng:
-
Cho hàm số \(y = - 3{x^4} + 4{x^2} - 2017\). Khẳng định nào sau đây là đúng?
-
Số điểm cực trị của hàm số \(y = {x^3} – 6{x^2} + 5x – 1\) là.
-
Đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) có tọa độ điểm cực đại là
-
Cho hàm số \(y = 3{x^4} - 4{x^3} + 2\). Khẳng định nào sau đây là đúng
-
Cho hàm số có đồ thị như hình vẽ bên dưới.
.png)
Mệnh đề nào sau đây sai?
-
Cho hàm số y=f(x) có \(f'\left( x \right) = \left( { - x + 2} \right){\left( {x + 1} \right)^4}\left( {x - 3} \right)\). Điểm cực tiểu của hàm số là
-
Cho hàm số \(y = - \frac{1}{3}{x^3} + 4{x^2} - 5x - 17\). Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là x1, x2. Khi đó, tích số có giá trị là
-
Hàm số \(y=x^{3}-3 x+1\) đạt cực đại tại x bằng :
-
Điểm cực đại của đồ thị hàm số \(y = 2{x^3} – 3{x^2} – 2\) là.
-
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = m{x^3} - 3m{x^2} + 3m - 3\) có hai điểm cực trị A, B sao cho \(2A{B^2} - \left( {O{A^2} + O{B^2}} \right) = 20\) (Trong đó O là gốc tọa độ).
-
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = \left( {x – 1} \right)\left( {x + 3} \right)\). Số điểm cực tiểu của hàm số là
-
Có giá trị của tham số m để đồ thị hàm số y = x4-4(m-1) x2+2m-1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều. Hỏi số nguyên nào gần với số m nhất?
-
Cho hàm số y=f(x) có bảng biến thiên như sau
Số điểm cực trị của đồ thị hàm số \(y=|f(x)|\) là:
-
Số cực trị của hàm số \(f\left( x \right) = - {{\rm{x}}^4}{\rm{ + }}\sqrt 5 {{\rm{x}}^2} + 2\) là
-
Biết rằng tập nghiệm của bất phương trình \(\sqrt{2 x+4}-2 \sqrt{2-x} \geq \frac{6 x-4}{5 \sqrt{x^{2}+1}} \text { là }[a ; b]\) Khi đó giá trị của biểu thức \(P=3 a-2 b\) bằng:
