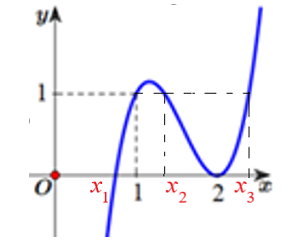
Cho hàm số \( f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \( g(x) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}\) có bao nhiêu tiệm cận đứng?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐKXĐ: x≥1,f(x)≠0,f(x)≠1
\( g(x) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}} = \frac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.f\left( x \right)\left( {f\left( x \right) - 1} \right)}}\)
Nhận xét:\( f\left( x \right) = a{x^3} + b{x^2} + cx + d\) là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy:
+) f(x)=0 có 2 nghiệm phân biệt x=x1(0<x1<1)(ktm) (nghiệm đơn) và x=2(nghiệm kép).
+) f(x)=1 có 3 nghiệm phân biệt x=1 (nghiệm đơn), x=x2(1<x2<2) (nghiệm đơn) và x=x3(x3>2) (nghiệm đơn).
Khi đó hàm số y=g(x) được viết dưới dạng :
\( g\left( x \right) = \frac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.{\mkern 1mu} a\left( {x - {x_1}} \right){{\left( {x - 2} \right)}^2}.{\mkern 1mu} a\left( {x - 1} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)}}\)
Do đó, đồ thị hàm số g(x) có 3 đường tiệm cận đứng là: x=x2,x=2,x=x3.
Đáp án cần chọn là: B