Cho hàm số f=f(x) ,bảng biến thiên của hàm số f'(x) như sau:
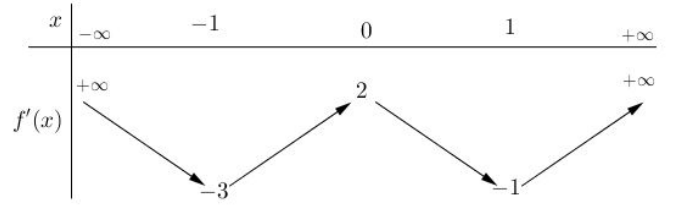
Số điểm cực trị của hàm số \(y=f\left(4 x^{2}+4 x\right)\) là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(\left(f\left(4 x^{2}+4 x\right)\right)^{\prime}=(8 x+4) f^{\prime}\left(4 x^{2}+4 x\right),\left(f\left(4 x^{2}+4 x\right)\right)^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=-\frac{1}{2} \\ f^{\prime}\left(4 x^{2}+4 x\right)=0 \end{array}\right.\)
Từ bảng biến thiên ta có \(f^{\prime}\left(4 x^{2}+4 x\right)=0 \Leftrightarrow\left[\begin{array}{l} 4 x^{2}+4 x=a_{1} \in(-\infty ;-1) \\ 4 x^{2}+4 x=a_{2} \in(-1 ; 0) \\ 4 x^{2}+4 x=a_{3} \in(0 ; 1) \\ 4 x^{2}+4 x=a_{4} \in(1 ;+\infty) \end{array}\right.\,\,\,(1)\)
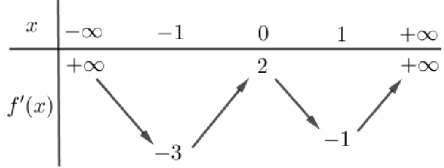
Xét \(g(x)=4 x^{2}+4 x, g^{\prime}(x)=8 x+4, g^{\prime}(x)=0 \Leftrightarrow x=-\frac{1}{2}\) ta có bảng biến thiên
Kết hợp bảng biến thiên của g(x) và hệ (1) ta thấy:
Phương trình \(4 x^{2}+4 x=a_{1} \in(-\infty ;-1)\) vô nghiệm.
Phương trình \(4 x^{2}+4 x=a_{2} \in(-1 ;0)\) tìm được hai nghiệm phân biệt khác \(-\frac{1}{2}\).
Phương trình \(4 x^{2}+4 x=a_{3 } \in(0 ; 1)\) tìm được thêm hai nghiệm mới phân biệt khác \(-\frac{1}{2}\) .
Phương trình \(4 x^{2}+4 x=a_{4} \in(1 ;+\infty)\) tìm được thêm hai nghiệm phân biệt khác \(-\frac{1}{2}\)
Vậy hàm số \(y=f\left(4 x^{2}+4 x\right)\) có tất cả 7 điểm cực trị.
Câu hỏi liên quan
-
Số điểm cực trị của hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 4\) là
-
Tọa độ điểm cực đại của đồ thị hàm số y = x3 – 3x2 + 4 là:
-
Cho hàm số \(f’\left( x \right) = {\left( {x – 2} \right)^2}\left( {{x^2} – 4x + 3} \right)\) với mọi \(x\in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của m để hàm số \(y = f\left( {{x^2} – 10x + m + 9} \right)\) có 5 điểm cực trị
-
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị A(0;0), B(1;1) thì các hệ số a, b, c, d có giá trị lần lượt là:
-
Điểm cực tiểu của đồ thị hàm số \(y = {x^4} - 3{x^2} - 1\) là:
-
Cho hàm số nào y=f(x) có \(f^{\prime}(x)=x^{2}(x-1)^{3}(3-x)(x-5)\) Số điểm cực tiểu của đồ thị hàm số là
-
Hàm số nào sau đây có cực trị?
-
Hàm số nào trong các hàm số sau đây không có cực trị?
-
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
-
Hàm số nào sau đây không có cực trị?
-
Điểm cực đại của hàm số \(y = {x^4} - 2{x^2} + 4\) là:
-
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
-
Hàm số \(y = - 3\sqrt[3]{{{x^2}}} + 2\) có bao nhiêu cực đại?
-
Số điểm cực đại của hàm số \(f\left( x \right) = - 5{{\rm{x}}^4} - 2{{\rm{x}}^2} + 3\) là
-
Cho hàm số f (x) xác định trên R , có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^3}{\left( {x - 2} \right)^5}{\left( {x + 3} \right)^3}\) . Số điểm cực trị của hàm số f(|x|) là:
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = - \frac{1}{2}{{\rm{x}}^4} + \frac{1}{3}{{\rm{x}}^2} - 2\) là
-
Tìm giá trị cực đại yCĐ của hàm số \(y=-x^{4}+2 x^{2}-5\)
-
Tìm tập hợp tất cả các giá trị thực của m để đồ thị hàm số y = x³ - 3mx² + 3m³ có có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48 (với O là gốc tọa độ)
-
Cho hàm số F(x) là một nguyên hàm của hàm số \(f ( x ) = 2019x ( x² - 4)( x² - 3x + 2)\). Khi đó số điểm cực trị của hàm số F(x) là
-
Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực tiểu trên khoảng \(\left( {a;b} \right)\)?
.jpg.png)
