Đề thi HK1 môn Toán 10 CTST năm 2022-2023
Trường THPT Lương Thế Vinh
-
Câu 1:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. ∀x∈R,x≤x2∀x∈R,x≤x2
B. ∀x∈R,|x|<3⇔x<3∀x∈R,|x|<3⇔x<3
C. ∀n∈N,n2+1∀n∈N,n2+1chia hết cho 3
D. ∃a∈Q,a2=2∃a∈Q,a2=2
-
Câu 2:
Cho mệnh đề “∀x∈R,x2−x+2023<0∀x∈R,x2−x+2023<0”. Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề đã cho?
A. ∀x∈R,x2−x+2023≥0∀x∈R,x2−x+2023≥0
B. ∃x∈R,x2−x+2023<0∃x∈R,x2−x+2023<0
C. ∃x∈R,x2−x+2023≥0∃x∈R,x2−x+2023≥0
D. ∀x∈R,x2−x+2023>0∀x∈R,x2−x+2023>0
-
Câu 3:
Cho A={1,2,3}A={1,2,3}.Trong các khẳng định sau, khẳng định nào sai:
A. ∅⊂A∅⊂A
B. 1∈A1∈A
C. {1,2}⊂A{1,2}⊂A
D. {3}∈A{3}∈A
-
Câu 4:
Các phần tử của tập hợp A={x∈R:2x2−5x+3=0}A={x∈R:2x2−5x+3=0} là
A. A={0}A={0}
B. A={1}A={1}
C. A={32}A={32}
D. A={1;32}A={1;32}
-
Câu 5:
Cho tập hợp A={−2,1,2,3,4}A={−2,1,2,3,4}, B={x∈N:x2−4=0}B={x∈N:x2−4=0}. Mệnh đề nào sau đây là đúng?
A. A∩B={2}A∩B={2}
B. A∩B={−2,2}A∩B={−2,2}
C. A∪B=BA∪B=B
D. A∖B={1,3,4}A∖B={1,3,4}
-
Câu 6:
Biểu diễn trên trục số các tập hợp [−4,3]∖[−2,1][−4,3]∖[−2,1] là hình nào dưới đây.
A.
B.
.png)
C.
.png)
D.
.png)
-
Câu 7:
Miền nghiệm của bất phương trình x+2y<4x+2y<4 là nửa mặt phẳng không chứa điểm nào trong các điểm sau?
A. (0;0)(0;0)
B. (0;0)(0;0)
C. (4;2)(4;2)
D. (1;−1)(1;−1)
-
Câu 8:
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình {2x−5y−1>02x+y+5>0x+y+1<0?
A. (0;0)
B. (1;0)
C. (0;−2)
D. (0;2)
-
Câu 9:
Để điều tra các con trong mỗi gia đình của một chung cư gồm 100 gia đình . Người ta chọn ra 20 gia đình ở tầng 4 và thu được mẫu số liệu sau đây : 2 4 2 1 3 5 1 1 2 3 1 2 2 3 4 1 1 2 3 4. Kích thước mẫu là bao nhiêu?
A. 5
B. 20
C. 4
D. 100
-
Câu 10:
Thống kê điểm thi môn toán trong một kỳ thi của 400 HS. Người ta thấy có 80 bài được điểm 7. Hỏi tần suất của giá trị xi=7là bao nhiêu?
A. 80%
B. 36%
C. 20%
D. 10%
-
Câu 11:
Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
Số trung bình là?
A. 6,1
B. 6,5
C. 6,7
D. 6,9
-
Câu 12:
Chọn câu đúng trong bốn phương án trả lời đúng sau đây. Độ lệch chuẩn là :
A. Bình phương của phương sai
B. Một nửa của phương sai
C. Căn bậc hai của phương sai
D. Không phải là các công thức trên.
-
Câu 13:
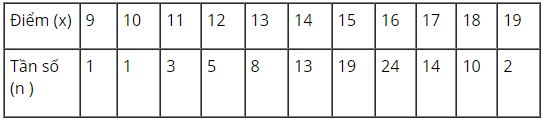
100 học sinh tham dự kì thi học sinh giỏi toán ( thang điểm là 20 ) . Kết quả cho trong bảng sau:
Số trung vị của bảng trên là :
A. 14,23
B. 15,28
C. 15,50
D. 16,50
-
Câu 14:
100 học sinh tham dự kì thi học sinh giỏi toán (thang điểm là 20) . Kết quả cho trong bảng sau:
Phương sai là:
A. 17,7
B. 15
C. 16
D. 15,50
-
Câu 15:
Tìm tập xác định D của hàm số y=3x−12x−2.
A. D=R
B. D=(1;+∞)
C. D=R∖{1}
D. D=[1;+∞)
-
Câu 16:
Tìm tập xác định D của hàm số y=√2−x+√x+2x.
A. D=[−2;2].
B. D=(−2;2)∖{0}.
C. D=[−2;2]∖{0}.
D. D=R.
-
Câu 17:
Cho hàm số y=f(x)=|−5x|. Khẳng định nào sau đây là sai?
A. f(−1)=5
B. f(2)=10
C. f(−2)=10
D. f(15)=−1
-
Câu 18:
Điểm nào sau đây thuộc đồ thị hàm số y=√x2−4x+4x.
A. A(2;0)
B. B(3;3)
C. C(1;−1)
D. D(−1;3)
-
Câu 19:
Giá trị nhỏ nhất của hàm số y=x−2√x+2 là:
A. – 4
B. – 3
C. – 2
D. - 1
-
Câu 20:
Cho hàm số y=2x2+6x+3 có đồ thị (P). Trục đối xứng của (P) là:
A. x=−32
B. x=−23
C. x=2
D. x=−2
-
Câu 21:
Giá trị của cos60o+sin30o bằng bao nhiêu?
A. √32
B. √3
C. √33
D. 1
-
Câu 22:
Tam giác ABC có a=8,c=3,ˆB=600. Độ dài cạnh b bằng bao nhiêu?
A. 49.
B. √97
C. 7.
D. √61.
-
Câu 23:
Cho tam giác ABC có a2=b2+c2−bc. Số đo góc A là
A. 300
B. 600
C. 450
D. 900
-
Câu 24:
Cho tam giác ABC có góc ^BAC=60∘ và cạnh BC=√3. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
A. R=4
B. R=1
C. R=2
D. R=3
-
Câu 25:
Chọn phát biểu sai:
A. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi →AB=k→BC,k≠0
B. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi →AC=k→BC,k≠0
C. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi →AB=k→AC,k≠0
D. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi →AB=k→AC
-
Câu 26:
Tính tổng →MN+→PQ+→RN+→NP+→QR
A. →MR.
B. →MN.
C. →PR.
D. →MP.
-
Câu 27:
Gọi O là tâm hình bình hành ABCD. Đẳng thức nào sau đây sai?
A. →OA−→OB=→CD.
B. →OB−→OC=→OD−→OA.
C. →AB−→AD=→DB.
D. →BC−→BA=→DC−→DA.
-
Câu 28:
Nếu G là trọng tâm tam giác ABC thì đẳng thức nào sau đây đúng.
A. →AG=32(→AB+→AC)
B. →AG=13(→AB+→AC)
C. →AG=23(→AB+→AC)
D. →AG=13(→AB+→AC)
-
Câu 29:
Cho tam giác ABC đều cạnh 4 cm. Giá trị của tích vô hướng →AB.→BC.
A. 8
B. – 8
C. 4
D. - 4
-
Câu 30:
Cho tam giác ABC. H là trung điểm của BC. Tính |→CA−→HC|.
A. |→CA−→HC|=a2.
B. |→CA−→HC|=3a2.
C. |→CA−→HC|=2√3a3.
D. |→CA−→HC|=a√72.
-
Câu 31:
Mệnh đề nào sau đây đúng?
A. 0={0}
B. 0∈{0}
C. 0⊂{0}
D. 0=∅
-
Câu 32:
Biết rằng P⇒Q là mệnh đề đúng. Mệnh đề nào sau đây đúng?
A. P là điều kiện cần để có Q
B. P là điều cần đủ để có Q
C. Q là điều kiện cần và đủ để có P
D. Q là điều kiện đủ để có P
-
Câu 33:
Cho hàm số y=f(x)=2(x+1)(x−3)+2x−6. Giá trị của hàm số khi x=3 là:
A. 8
B. 0
C. -6
D. 3
-
Câu 34:
Bạn Danh để dành được 900 nghìn đồng. Trong một đợt ủng hộ trẻ em mồ côi, Danh đã lấy ra x tờ 50 nghìn đồng, y tờ tiền 100 nghìn đồng để trao tặng. Một bất phương trình mô tả điều kiện ràng buộc với x, y là:
A. 50x+100y≤900
B. 50x+100y≥900
C. 100x+50y≤900
D. x+y=900
-
Câu 35:
Khẳng định nào sau đây là đúng?
A. sinα=sin(180∘−α)
B. cosα=cos(180∘−α)
C. tanα=tan(180∘−α)
D. cotα=cot(180∘−α)
-
Câu 36:
Trong các khẳng định sau đây, khẳng định nào sai?
A. cos45∘=sin45∘
B. cos45∘=sin135∘
C. cos30∘=sin120∘
D. sin60∘=cos120∘
-
Câu 37:
Cho hình chữ nhật ABCD có AB=3,BC=4. Độ dài của vectơ →AC là:
A. 5
B. 6
C. 7
D. 9
-
Câu 38:
Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ →OC có điểm đầu và điểm cuối la các đỉnh của lục giác là:
A. 2
B. 3
C. 4
D. 6
-
Câu 39:
Số quy tròn của 45,6534 với độ chính xác d=0,01 là:
A. 45,65;
B. 45,6;
C. 45,7;
D. 45.
-
Câu 40:
Cho biết 3√3=1,44224957.... Số gần đúng của 3√3 với độ chính xác 0,0001 là:
A. 1,4422;
B. 1,4421;
C. 1,442;
D. 1,44.




.JPG)
.JPG)











