Đề thi giữa HK1 môn Toán 9 năm 2020
Trường THCS Trần Hưng Đạo
-
Câu 1:
Tìm điều kiện xác định của biểu thức \(\sqrt {x - 8} \).
A. \(x \ge 8\)
B. \(x > 8\)
C. \(x < 8\)
D. \(x \le 8\)
-
Câu 2:
Đường thẳng nào sau đây không song song với đường thẳng y = 7x + 3?
A. \(y = 7x\)
B. \(y = 4 - 7x\)
C. \(y = 7x + 1\)
D. \(y = - 1 + 7x\)
-
Câu 3:
Giá trị của biểu thức \(\sqrt {0,{{04.30}^2}}\) bằng bao nhiêu?
A. 6
B. 0,12
C. 12
D. 0,24
-
Câu 4:
Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Khi đó độ dài đoạn thẳng BC bằng
A. \(10cm\)
B. \(\sqrt {14} cm\)
C. \(\sqrt 2 cm\)
D. \(14cm\)
-
Câu 5:
Cho tam giác ABC vuông tại A, đường cao AH. Hệ thức nào trong các hệ thức sau là đúng?
A. \(AH.HB = CB.CA\)
B. \(A{B^2} = CH.BH\)
C. \(A{C^2} = BH.BC\)
D. \(AH.BC = AB.AC\)
-
Câu 6:
Cho tam giác MNP vuông ở \(M,\,MN = 4a; MP = 3a.\) Khi đó, \(\tan P\) bằng bao nhiêu?
A. \(\dfrac{3}{4}\)
B. \(\dfrac{4}{3}\)
C. \(\dfrac{3}{5}\)
D. \(\dfrac{4}{5}\)
-
Câu 7:
Biểu thức \(\displaystyle \sqrt {1 - 2x}\) xác định khi nào?
A. \(\displaystyle x \ge \dfrac{1}{2}\)
B. \(\displaystyle x \le \dfrac{1}{2}\)
C. \(\displaystyle x > \dfrac{1}{2}\)
D. \(\displaystyle x < \dfrac{1}{2}\)
-
Câu 8:
Tìm điều kiện xác định của biểu thức \(\displaystyle \dfrac{{\sqrt x + 1}}{{x - \sqrt x }}\).
A. \(\displaystyle x \ne 0\)
B. \(\displaystyle x > 0,x \ne 1\)
C. \(\displaystyle x \ge 0\)
D. \(\displaystyle x \ge 0,x \ne 1\)
-
Câu 9:
Biểu thức \(\displaystyle \sqrt {\dfrac{1}{{x - 1}}} + \sqrt {2 - x}\) có nghĩa khi nào?
A. \(\displaystyle x > 2\)
B. \(\displaystyle x < 1\)
C. \(\displaystyle 1 < x \le 2\)
D. \(\displaystyle x \le 2,x \ne 1\)
-
Câu 10:
Căn bậc hai số học của 64 là bao nhiêu?
A. 8 và -8
B. - 8
C. 8
D. 32
-
Câu 11:
Kết quả phép tính \(\displaystyle \sqrt {{{(\sqrt 3 - \sqrt 2 )}^2}}\) là bằng mấy ?
A. \(\displaystyle \sqrt 3 - \sqrt 2\)
B. \(\displaystyle \sqrt 2 - \sqrt 3\)
C. \(\displaystyle \pm (\sqrt 3 - \sqrt 2 )\)
D. 1
-
Câu 12:
Kết quả của phép tính \(\displaystyle (2\sqrt 3 + \sqrt 2 )(2\sqrt 3 - \sqrt 2 )\) là bao nhiêu?
A. \(\displaystyle 4\sqrt 3\)
B. \(\displaystyle 2\sqrt 2\)
C. 10
D. 14
-
Câu 13:
Tính giá trị của biểu thức \(\displaystyle {1 \over {2 + \sqrt 3 }} - {1 \over {2 - \sqrt 3 }}\)
A. 4
B. 0
C. \(\displaystyle - 2\sqrt 3\)
D. \(\displaystyle 2\sqrt 3\)
-
Câu 14:
Tính giá trị của biểu thức \(\displaystyle \sqrt 3 - \sqrt {48} + \sqrt {12}\).
A. \(\displaystyle - \sqrt 3 \)
B. \(\displaystyle \sqrt 3 \)
C. \(\displaystyle - 2\sqrt 3\)
D. \(\displaystyle 2\sqrt 3\)
-
Câu 15:
Tính giá trị của biểu thức \(\displaystyle \sqrt {{{(1 - \sqrt 2 )}^2}} - \sqrt {{{(1 + \sqrt 2 )}^2}} \)
A. 0
B. - 2
C. \(\displaystyle - \sqrt 2\)
D. \(\displaystyle - 2\sqrt 2\)
-
Câu 16:
Giá trị của biểu thức \(\displaystyle \)\(\displaystyle \left( {\sqrt {27} - 3\sqrt {\dfrac{4}{3}} + \sqrt {12} } \right):\sqrt 3 \) bằng bao nhiêu?
A. \(\displaystyle \sqrt 3\)
B. \(\displaystyle 2\sqrt 3 \)
C. \(\displaystyle - 2\sqrt 3\)
D. 3
-
Câu 17:
Tìm kết quả rút gọn của biểu thức \(\displaystyle \dfrac{{\sqrt {{x^2} - 6x + 9} }}{{x - 3}}\) với \(\displaystyle x > 3\)
A. - 1
B. 1
C. \(\displaystyle \pm 1\)
D. Kết quả khác
-
Câu 18:
Kết quả rút gọn của biểu thức \(\displaystyle {x^2}{y^2}.\sqrt {\dfrac{9}{{{x^2}{y^4}}}} \)
A. \(\displaystyle 3xy\)
B. \(\displaystyle {x^2}y\)
C. \(\displaystyle -3x\)
D. \(\displaystyle -3xy\)
-
Câu 19:
Tìm tất cả các giá trị của x thỏa mãn \(\displaystyle \sqrt {4{x^2} + 4x + 1} = 7\)
A. \(x=3\)
B. \(x = \dfrac{{ - 7}}{2}\)
C. \(x=-3\)
D. \(x=-4;x=3\)
-
Câu 20:
Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?
A. AH2 = AB.AC
B. AH2 = BH.CH
C. AH2 = AB.BH
D. AH2 = CH.BC
-
Câu 21:
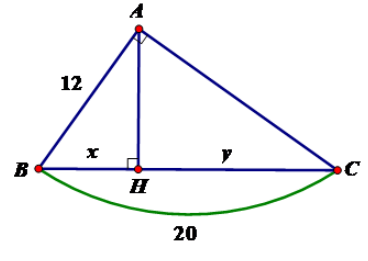
Tính x, y trong hình vẽ sau:
A. \(x = 7,2; y = 11,8\)
B. \(x = 7; y = 12\)
C. \(x = 7,2; y = 12,8\)
D. \(x = 7,2; y = 12\)
-
Câu 22:
Cho α và β là góc nhọn bất kỳ thỏa mãn α + β = 90° . Chọn khẳng định đúng.
A. \(α + β = 90°\)
B. \(tanα = cotβ\)
C. \(tanα = cosα\)
D. \(tanα = tanβ\)
-
Câu 23:
Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?
A. MN = MP.sinP
B. MN = MP.cosP
C. MN = MP.tanP
D. MN = MP.cotP
-
Câu 24:
Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?
A. \(b = a.sinB = a.cosC\)
B. \(a = c.tanB = c.cotC\)
C. \(a^2 = b^2 + c^2\)
D. \(c = a.sinC = a.cosB\)
-
Câu 25:
Tam giác ABC vuông tại A; đường cao AH; biết HB = 25cm; HC = 64 cm. Tính góc B
A. 42°
B. 32°
C. 51°
D. 58°
-
Câu 26:
Cho tam giác ABC vuông tại A có BC = 72 cm và góc B = 58°. Tính AB và AC?
A. 38,15 và 61,06
B. 36,06 và 62,01
C. 37,09 và 60,19
D. 39,01 và 62,93
-
Câu 27:
Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất
A. 58°45'
B. 59°50'
C. 59°45'
D. 58°4'
-
Câu 28:
Nhà bạn Minh có một chiếc thang dài 4m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là 65° (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
A. 1,76 m
B. 1,71 m
C. 1,68 m
D. 1,69 m
-
Câu 29:
Kết quả của phép tính \(\sqrt[3]{{27}}:\sqrt[3]{8}\) ?
A. \(\frac{{27}}{8}\)
B. \(\frac{3}{2}\)
C. \(\frac{9}{2}\)
D. Một kết quả khác
-
Câu 30:
Tìm x biết \(\sqrt[3]{{2{\rm{x}} + 1}} = 3\)
A. \(x = 1\)
B. \(x = 13\)
C. \(x = 4\)
D. \(x = 6\)