GTNN của biểu thức \(F(x;y) = 5x - 3y\), với điều kiện \(\left\{ \begin{array}{*{35}{l}} x\ge 0 \\ 0\le y\le 5 \\ x+y-2\ge 0 \\ 3x-y\le 6 \\ \end{array} \right.\text{ }\)?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\0 \le y \le 5\\x + y - 2 \ge 0\\3x - y \le 6\end{array} \right.\)
Biểu diễn miền nghiệm của hệ, ta được:
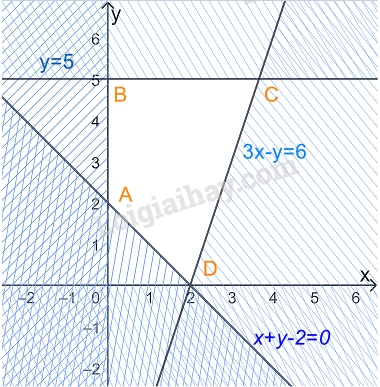
Miền nghiệm là miền tứ giác ABCD trong đó \(A\left( {0;2} \right),{\rm{ }}B\left( {0;5} \right),{\rm{ }}C\left( {\frac{{11}}{3};5} \right),D(2;0)\)
Thay tọa độ các điểm A, B, C, D vào \(F(x;y) = 5x - 3y\) ta được
\(F(0;2) = 5.0 - 3.2 = - 6\)
\(F(0;5) = 5.0 - 3.5 = - 15\)
\(F\left( {\frac{{11}}{3};5} \right) = 5.\frac{{11}}{3} - 3.5 = \frac{{10}}{3}\)
\(F(2;0) = 5.2 - 3.0 = 10\)
Vậy giá trị lớn nhất của F bằng 10.
Chọn B.
Đề thi giữa HK1 môn Toán 10 năm 2023-2024
Trường THPT Phan Bội Châu














