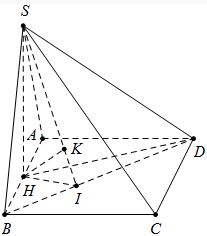
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \frac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Từ H kẻ HI vuông góc với BD \(\left( {I \in BD} \right)\) và \(HK \bot SI\)
Suy ra \(HK \bot \left( {SBD} \right).\)
Ta có:
\(SH = \sqrt {S{D^2} - H{D^2}} = a\sqrt 3\) và
\(HI = \frac{{AC}}{4} = \frac{{a\sqrt 2 }}{4}\)
Suy ra \(HK = \frac{{SH.IH}}{{\sqrt {S{H^2} + I{H^2}} }} \)
\(= \frac{{\frac{{{a^2}\sqrt 6 }}{4}}}{{\frac{{5a\sqrt 2 }}{4}}} = \frac{{a\sqrt 3 }}{5}\)
Do đó chiều cao của khối chóp H.SBD là:
\(h = \frac{{a\sqrt 3 }}{5}.\)
Đề thi giữa HK1 môn Toán 12 năm 2022-2023
Trường THPT Trần Hưng Đạo
Câu hỏi liên quan
-
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 1}}{{2x - 1}}?\)
-
Gọi M và m lần lượt là GTLN và GTNN của hàm số \(y = x\sqrt {1 - {x^2}}\) trên tập xác định. Tính M-m.
-
Hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là đúng?
-
Phương trình x4 – 2x2 – 3 + m = 0 có 4 nghiệm phân biệt khi và chỉ khi:
-
Tìm tất cả các giá trị nguyên của tham số thực m để hàm số \(y = \frac{1}{3}{x^3} + \frac{1}{2}m{x^2}\) có điểm cực đại x1 điểm cực tiểu x2 sao cho \(- 2 < {x_1} < - 1;\,\,1 < {x_2} < 2.\)
-
Cho hình chóp S.ABC có đáy là ABC là tam giác vuông cân tại B và BA = BC = a. Cạnh bên \(SA = a\sqrt 3\) vuông góc với mặt phẳng (ABC). Tính thể tích V của khối chóp S.ABC.
-
Cho hàm số y = f(x) xác định trên khoảng \((2;+\infty )\) và thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1.\) Khẳng định nào sau đây là đúng?
-
Cho hàm số \(y = \frac{x}{{x - 1}}.\) Mệnh đề nào sau đây là đúng?
-
Khối đa diện đều có 12 mặt thì có bao nhiêu cạnh?
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} - m{x^2} + 3x + 4\) đồng biến trên \(\mathbb{R}\).
-
Cho hình chóp S.ABC có đáy là tam giác vuông cân có cạnh huyền là 4a và thể tích bằng \(a^3\). Tính chiều cao h của khối chóp S.ABC.
-
Hình lăng trụ có thể có số cạnh là số nào sau đây?
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD.
-
Cho khối lăng trụ tam giác ABC.A’B’C’ có thể tích V. Tính thể tích \(V_1\) của khối tứ diện A’B’C'C.
-
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \({x^3} + {x^2} + x = m{\left( {{x^2} + 1} \right)^2}\) có nghiệm thuộc đoạn [0;1].
-
Hình vẽ bên là đồ thị của một hàm trùng phương y=f(x). Tìm giá trị của m để phương trình |f(x)|=m có 4 nghiệm đôi một khác nhau.
-
Tìm giá trị lớn nhất M của hàm số \(y = \cos 2x + 4\cos x + 1.\)
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của cạnh SD. Biết rằng khối chóp S.ABCD có thể tích bằng \(a^3\) và tam giác MAC là tam giác đều cạnh a, hãy tính khoảng cách d từ điểm S đến mặt phẳng (MAC).
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng \(a^3\). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
-
Cho hàm số \(y = {x^2}(3 - x).\) Mệnh đề nào sau đây là đúng?
