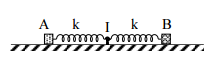
Trên mặt phẳng nằm ngang có hai con lắc lò xo. Các lò xo có cùng độ cứng k, cùng chiều dài tự nhiên là 32 cm. Các vật nhỏ A và B có khối lượng lần lượt là m và 4m. Ban đầu, A và B được giữ ở vị trí sao cho lò xo gắn với A bị dãn 8 cm còn lò xo gắn với B bị nén 8 cm. Đồng thời thả nhẹ để hai vật dao động điều hòa trên cùng một đường thẳng đi qua giá I cố định (hình vẽ). Trong quá trình dao động, khoảng cách lớn nhất và nhỏ nhất giữa hai vật có giá trị lần lượt là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình dao động của vật A là
\( {x_1} = 8\cos (2\omega t + \pi )\)
Phương trình dao động của vật B là
\(x_2=8cos(ωt+π)\)
Mặt khác
\( AI = 32 - {x_1};BI = 32 + {x_2} = > AB = 64 + {x_2} - {x_1}\)
Ta có:
\(\begin{array}{*{20}{l}} {d = {x_2} - {x_1} = 8\cos (\omega t + \pi ) - 8\cos (2\omega t + \pi )}\\ {\cos \omega t = a = > d = 8(\cos 2\omega t - \cos \omega t) = 8(2{a^2} - a - 1)}\\ {f(a) = 2{a^2} - a - 1/\left( { - 1;1} \right)}\\ {f' = 4a - 1,f' = 0 = > a = \frac{1}{4}} \end{array}\)
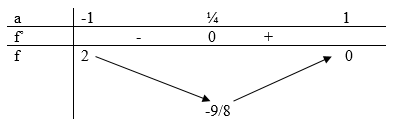
Xét bảng biến thiên sau
Từ bảng biến thiên ta có:
\(\begin{array}{*{20}{l}} { - \frac{9}{8} \le f(a) \le 2 = > AB = 64 + d}\\ { = > 64 + 8.\left( { - \frac{9}{8}} \right) \le AB \le 64 + 8.2}\\ { = > 55 \le AB \le 80} \end{array}\)