Một sóng cơ lan truyền trên sợi dây với chu kì T, biên độ A. Ở thời điểm t1, li độ các phần tử tại B và C tương ứng là –24 mm và +24 mm; các phần tử tại trung điểm D của BC đang ở vị trí cân bằng. Ở thời điểm t2, li độ tại các phần tử B và C cùng là +10 mm thì phần tử ở D cách vị trí cân bằng của nó
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
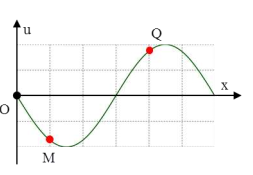
Báo saiTại thời điểm t1, li độ các phần tử tại B và C tương ứng là –24 mm và +24 mm; các phần tử tại trung điểm D của BC đang ở vị trí cân bằng nên B và C sẽ nằm ở hai bó sóng khác nhau như hình vẽ.
Tại thời điểm t2, li độ tại các phần tử B và C cùng là +10 mm thì phần tử ở D sẽ nằm ở vị trí
đỉnh sóng như hình vẽ.
Dựa vào hai hình vẽ, ta thấy rằng từ thời điểm t1 đến thời điểm t2 sóng truyền được quãng đường là \(s=k\lambda +\frac{\lambda }{4}\) tương ứng với độ thay đổi của pha dao động là \(\Delta \varphi =k2\pi +\frac{\pi }{2}.\)
Li độ của B tại hai thời điểm t1 và t2:
+ Tại thời điểm t1: \({{u}_{B}}=A.\cos \left( \omega {{t}_{1}}+\varphi \right)=-24\Rightarrow \cos \left( \omega {{t}_{1}}+\varphi \right)=\frac{-24}{A}\text{ (1)}\)
+ Tại thời điểm t2:
\({{u}_{B}}=A.\cos \left( \omega {{t}_{2}}+\varphi \right)=A.\cos \left( \omega {{t}_{1}}+\varphi +k2\pi +\frac{\pi }{2} \right)=\sin \left( \omega {{t}_{1}}+\varphi \right)=10\)
\(\Rightarrow \sin \left( \omega {{t}_{1}}+\varphi \right)=\frac{10}{A}\text{ (2)}\)
Ta lấy (1)2 + (2)2 vế theo vế: \(1=\frac{576}{{{A}^{2}}}+\frac{100}{{{A}^{2}}}\Rightarrow A=\sqrt{676}=26\text{ cm}\)
Vậy tại thời điểm t2, D nằm cách vị trí cân bằng 26 cm.
Câu hỏi liên quan
-
Một nguồn sóng cơ dao động điều hòa theo phương trình \(u=acos\left( 10\pi t\text{ }+\frac{\pi }{2} \right)cm.\) Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền dao động lệch pha nhau \(\frac{\pi }{3}\) là 5 m. Vận tốc truyền sóng là
-
Cường độ âm được xác định bởi:
-
Một sóng cơ học tại thời điểm t=0 có đồ thị là đường liền nét. Sau thời gian t, nó có đồ thị là đường đứt nét. Cho biết vận tốc truyền sóng là 4m/s, sóng truyền từ phải qua trái. Giá trị của t là:
-
Sóng ngang truyền trên sợi dây được căng ngang từ đầu O của dây. Li độ biến thiên theo hàm cosin với biên độ 2 cm và tần số 250 Hz. Pha ban đầu tại O bằng 0. Phương trình sóng tại O như thế nào?
-
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng λ. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước đang dao động. Biết \(OM=8\lambda ,ON=12\lambda\) và OM vuông góc ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
-
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm t0, một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử dây tại M và O dao động lệch pha nhau
.PNG)
-
Sóng cơ
-
Một song lan truyền dọc theo một dây đàn hồi thẳng, dài vô hạn. Hai điểm M, N cách nhau \(\frac{7\lambda }{4}\). Khi li độ tại M là 3 cm thì li độ tại N là -4 cm. Biên độ sóng trên dây bằng
-
Khi nói về sóng cơ, phát biểu nào dưới đây là sai?
-
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là: \(u=acos\omega t.\) Một điểm M cách nguồn đoạn 1/3 bước sóng ở thời điểm t = T/2 có độ dịch chuyển là 2 cm. Biên độ sóng là
-
Khi nói về sóng cơ, phát biểu nào sau đây sai?
-
Chọn phát biểu sai.
-
Để phân loại sóng ngang và sóng dọc người ta dựa vào
-
Sóng dừng là hiện tượng
-
Khi nói về sóng cơ, phát biểu nào sau đây sai?
-
Trong thí nghiệm về hiện tượng sóng trên mặt nước, nếu gọi bước sóng là λ, thì khoảng cách giữa n vòng tròn sóng (gợn nhô) liên tiếp nhau sẽ là
-
Về sóng ngang tìm câu đúng. Sóng ngang là sóng
-
Thông thường vận tốc truyền sóng cơ học tăng dần khi truyền lần lượt qua các môi trường
-
Sóng dọc là sóng có phương dao động của các phần tử môi trường và phương truyền sóng hợp với nhau một góc
-
Sóng dọc truyền được trong các môi trường
